The Universe of Aristotle and Ptolemy, and the Role of Eratosthenes

The Universe of
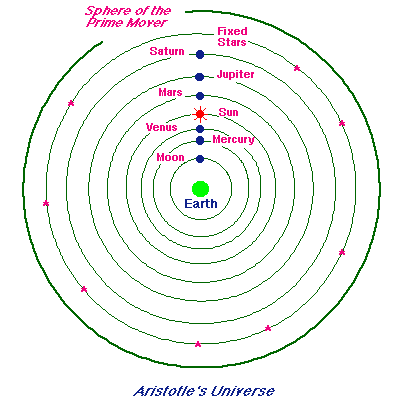
Aristotle and Ptolemy and the Role of Eratosthenes

Aristotle and Eratosthenes

Although Aristotle was not a scientist, it is important to note that he did point out that the Earth had to be sphere since its shadow was always circular. This was in fact a key scientific insight. It allowed Eratosthenes around 200 BC to calculate the circumference of the Earth. The method was very clever for the time:
The southern Egyptian city of Syene had a well in which sun-rays fell directly vertical during the summer solstice. The sun was therefore at the Zenith there during this time.
However, during the same time in Alexandria, the sun was 7 degrees south of the Zenith (1/50 of the circumference of the sky). Now since the Earth was spherical (from Aristotle) the 7 degree angle subtended at the Earths surface divided by 360 degrees equaled the distance between Alexandria and Syene divided by the Earth's circumference. That is, by using
7 / 360 = distance / circumference
he could measure the distance (in units of stadia) and then infer the circumference in stadia (about 40,000). Hard to infer the actual distance in standard modern units since stadia are of varying sizes, but the technique was clever at the time and if one uses typical stadium lengths of the time the estimate was only off by a number bewteen 4 and 14 percent.
Aristotle's Spheres
The celestial sphere that we introduced previously is a convenient "fiction" to locate objects in the sky. However, the Greek philosopher Aristotle (many of Aristotle's works are available at the Internet Classics Archive) proposed that the heavens were literally composed of 55 concentric, crystalline spheres to which the celestial objects were attached and which rotated at different velocities (but the angular velocity was constant for a given sphere), with the Earth at the center. The following figure illustrates the ordering of the spheres to which the Sun, Moon, and visible planets were attached.

(The diagram is not to scale, and the planets are aligned for convenience in illustration; generally they were distributed around the spheres.) There were additional "buffering" spheres that lay between the spheres illustrated. The sphere of the stars lay beyond the ones shown here for the planets; finally, in the Aristotelian conception there was an outermost sphere that was the domain of the "Prime Mover". The Prime Mover caused the outermost sphere to rotate at constant angular velocity, and this motion was imparted from sphere to sphere, thus causing the whole thing to rotate.
By adjusting the velocities of these concentric spheres, many features of planetary motion could be explained. However, the troubling observations of varying planetary brightness and retrograde motion could not be accommodated: the spheres moved with constant angular velocity, and the objects attached to them were always the same distance from the earth because they moved on spheres with the earth at the center.

Epicycles and Planetary Motion
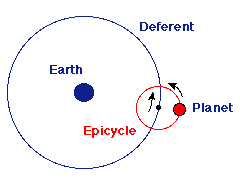The "solution" to these problems came in the form of a clever proposal: planets were attached, not to the concentric spheres themselves, but to circles attached to the concentric spheres, as illustrated in the adjacent diagram. These circles were called "Epicycles", and the concentric spheres to which they were attached were termed the "Deferents". Then, the centers of the epicycles executed uniform circular motion as they went around the deferent at uniform angular velocity, and at the same time the epicycles (to which the planets were attached) executed their own uniform circular motion.
The net effect was as illustrated in the following animation. As the center of the epicycle moves around the deferent at constant angular velocity, the planet moves around the epicycle, also at constant angular velocity. The apparent position of the planet on the celestial sphere at each time is indicated by the line drawn from the earth through the planet and projected onto the celestial sphere. The resulting apparent path against the background stars is indicated by the blue line.

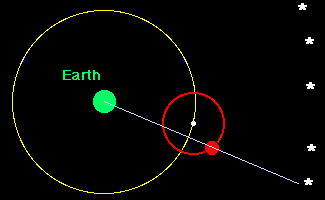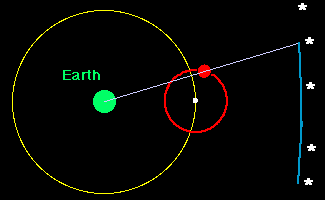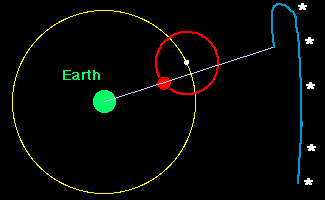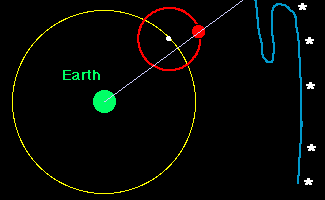
Now, in this tortured model one sees that it is possible to have retrograde motion and varying brightness, since at times as viewed from the earth the planet can appear to move "backward" on the celestial sphere. Obviously, the distance of the planet from the Earth also varies with time, which leads to variations in brightness. Thus, the idea of uniform circular motion is saved (at least in some sense) by this scheme, and it allows a description of retrograde motion and varying planetary brightness.

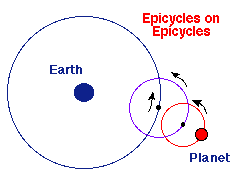More Sophisticated Epicycles: The Ptolemaic Universe
In practice, even this was not enough to account for the detailed motion of the planets on the celestial sphere. In more sophisticated epicycle models further "refinements" were introduced:

In some cases, epicycles were themselves placed on epicycles, as illustrated in the adjacent figure.

In actual models, the center of the epicycle moved with uniform circular motion, not around the center of the deferent, but around a point that was displaced by some distance from the center of the deferent.
That ancient astronomers could convince themselves that this elaborate scheme still corresponded to "uniform circular motion" is testament to the power of three ideas that we now know to be completely wrong, but that were so ingrained in the astronomers of an earlier age that they were essentially never questioned:

All motion in the heavens is uniform circular motion.

The objects in the heavens are made from perfect material, and cannot change their intrinsic properties (e.g., their brightness).

The Earth is at the center of the Universe.
These ideas concerning uniform circular motion and epicycles were cataloged by Ptolemy in 150 A.D. His book was called the "Almagest" (literally, "The Greatest"), and this picture of the structure of the Solar System has come to be called the "Ptolemaic Universe".

Medieval Aristotelian Astronomy
By the Middle Ages, such ideas took on a new power as the philosophy of Aristotle (newly rediscovered in Europe) was wedded to Medieval theology in the great synthesis of Christianity and Reason undertaken by philosopher-theologians such as Thomas Aquinas. The Prime Mover of Aristotle's universe became the God of Christian theology, the outermost sphere of the Prime Mover became identified with the Christian Heaven, and the position of the Earth at the center of it all was understood in terms of the concern that the Christian God had for the affairs of mankind.
Thus, the ideas largely originating with pagan Greek philosophers were baptized into the Catholic church and eventually assumed the power of religious dogma: to challenge this view of the Universe was not merely a scientific issue; it became a theological one as well, and subjected dissenters to the considerable and not always benevolent power of the Church.