The Curve of
Binding Energy

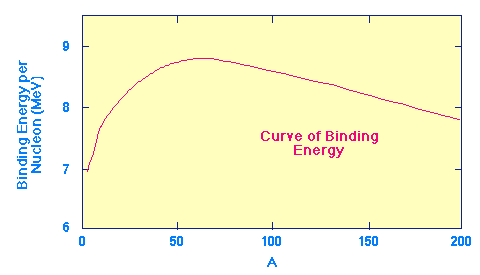
The key to energy production in stars lies in what nuclear physicists call the curve of binding energy, which is illustrated in the following figure.

Curve of binding energy.


This plot shows the amount of binding energy per nucleon (A nucleon is either a neutron or a proton. The nucleon number is the sum of the number of neutrons plus protons in a nucleus; thus, it is equal to the atomic mass number) as a function of the atomic mass number A. The energy units are MeV, which stands for "million electron-volts", a standard unit of energy in nuclear physics.

This curve indicates how stable atomic nuclei are; the higher the curve the more stable the nucleus. Notice the characteristic shape, with a peak near A=60. These nuclei (which are near iron in the periodic table and are called the iron peak nuclei) are the most stable in the Universe. The shape of this curve suggests two possibilites for converting significant amounts of mass into energy. Note that this is the "upside down" version of the similar graph in text. There the vertical scale increases downward, here it increases upward.

Fission Reactions

From the curve of binding energy, the heaviest nuclei are less stable than the nuclei near A=60. This suggests that energy can be released if heavy nuclei split apart into smaller nuclei having masses nearer A=60. This process is called fission. It is the process that powers atomic bombs and nuclear power reactors.

Fusion Reactions

The curve of binding energy suggests a second way in which energy could be released in nuclear reactions. The lightest elements (like hydrogen and helium) have nuclei that are less stable than heavier elements up to A~60. Thus, sticking two light nuclei together to form a heavier nucleus can release energy. This process is called fusion, and is the process that powers hydrogen (thermonuclear) bombs and (perhaps eventually) fusion energy reactors.

In both fission and fusion reactions the total masses after the reaction are less than those before. The "missing mass" appears as energy, with the amount given by the famous Einstein equation.

Stellar Energy Production

Both fission and fusion reactions have the potential to convert a small amount of mass into a large amount of energy and could conceivably account for the energy sources of stars. However, stars are made from light elements (mostly hydrogen and helium). Thus, fission cannot be initiated in stars as a source of energy, but fusion is quite possible if the right conditions prevail. As we shall see, these conditions can be found in the cores of stars, and thermonuclear fusion is the primary source of stellar energy.