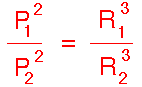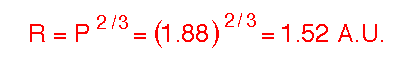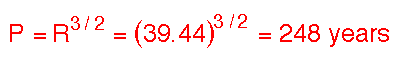Esta pagina en Español (Thanks to Rosselyn Evies)
 Johannes Kepler: The
Johannes Kepler: The
Laws of Planetary Motion
In the interplay between quantitative observation and theoretical construction
that characterizes the development of modern science,
we have seen that Brahe
was the master of the first but was deficient in the
second. The next great development in the history of astronomy was the
theoretical intuition of Johannes Kepler (1571-1630), a German who went to
Prague to become Brahe's assistant.
Brahe's Data and Kepler
 Kepler and Brahe did not get along well. Brahe apparently mistrusted Kepler,
fearing that his bright young assistant might eclipse him as the premiere
astonomer of his day. He therefore let Kepler see only part of his voluminous
data.
Kepler and Brahe did not get along well. Brahe apparently mistrusted Kepler,
fearing that his bright young assistant might eclipse him as the premiere
astonomer of his day. He therefore let Kepler see only part of his voluminous
data.
He
set Kepler the task of understanding the orbit of the planet
Mars, which was
particularly troublesome. It is believed that part of the
motivation for giving the Mars problem to Kepler was that it was difficult, and
Brahe hoped it would occupy Kepler while Brahe worked on his theory of the
Solar System. In a supreme irony, it was precisely the Martian data that
allowed Kepler to formulate the correct laws of planetary motion,
thus eventually achieving a place in the development of astronomy far
surpassing that of Brahe.
Kepler and the Elliptical Orbits
Unlike Brahe, Kepler believed firmly in the
Copernican
system.
In retrospect, the reason that the orbit of Mars was particularly difficult was
that Copernicus had correctly placed the Sun at the center of the Solar System,
but had erred in assuming the orbits of the planets to be circles.
Thus, in the Copernican theory epicycles were still required to explain the
details of planetary motion.
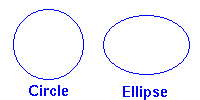 It fell to
Kepler to provide the final piece of the puzzle: after a long struggle, in
which he tried mightily to avoid his eventual conclusion, Kepler was
forced finally to the realization that
the orbits of the planets were not the circles demanded by Aristotle and
assumed implicitly by Copernicus, but were instead
the "flattened circles" that geometers call
ellipses
(See adjacent figure; the planetary orbits are only slightly
elliptical and are not as flattened as in this example.)
It fell to
Kepler to provide the final piece of the puzzle: after a long struggle, in
which he tried mightily to avoid his eventual conclusion, Kepler was
forced finally to the realization that
the orbits of the planets were not the circles demanded by Aristotle and
assumed implicitly by Copernicus, but were instead
the "flattened circles" that geometers call
ellipses
(See adjacent figure; the planetary orbits are only slightly
elliptical and are not as flattened as in this example.)
The irony noted above
lies in the realization that the difficulties with the
Martian orbit derive precisely
from the fact that the orbit of Mars was the most
elliptical of the planets for which Brahe had extensive data. Thus
Brahe had unwittingly given Kepler the very part of his data that
would allow Kepler to eventually formulate the correct theory of the Solar
System and thereby to banish Brahe's own theory!
Some Properties of Ellipses
Since the orbits of the planets are ellipses, let us review a few basic
properties of ellipses.
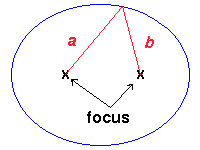 1. For an ellipse there are
two points called foci (singular: focus) such that the
sum of the distances to the foci from any point on the ellipse is a constant.
In terms of the diagram shown to the left,
with "x" marking the location of the foci, we
have the equation
1. For an ellipse there are
two points called foci (singular: focus) such that the
sum of the distances to the foci from any point on the ellipse is a constant.
In terms of the diagram shown to the left,
with "x" marking the location of the foci, we
have the equation
a + b = constant
that defines the ellipse in terms of the distances a and b.
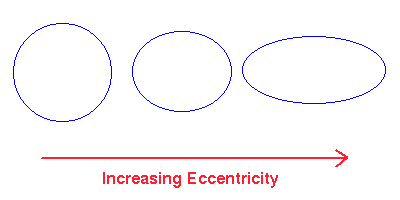
2. The amount of "flattening" of the ellipse is termed the
eccentricity. Thus, in the following figure the ellipses become more
eccentric from left to right. A circle may be viewed as a special case of an
ellipse with zero eccentricity, while as the ellipse becomes more flattened the
eccentricity approaches one.
Mathematically it is defined as the distance between foci divided
by the major axis length.
Thus, all ellipses have eccentricities lying between
zero and one.
 The orbits of the planets are ellipses but the eccentricities are so small for
most of the planets that
they look circular at first glance. For most of the planets
one must measure the geometry carefully to
determine that they are not circles, but ellipses of small
eccentricity. Pluto and Mercury are exceptions: their orbits are sufficiently
eccentric that they can be seen by inspection to not be circles.
The orbits of the planets are ellipses but the eccentricities are so small for
most of the planets that
they look circular at first glance. For most of the planets
one must measure the geometry carefully to
determine that they are not circles, but ellipses of small
eccentricity. Pluto and Mercury are exceptions: their orbits are sufficiently
eccentric that they can be seen by inspection to not be circles.
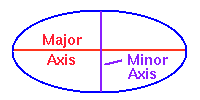 3. The long axis of the ellipse is called the major axis, while the
short axis is called the minor axis (adjacent figure). Half of the
major axis is termed a semimajor axis. The
length of a semimajor axis is often termed the size of the ellipse. It can
be shown that the average separation of a planet from the Sun as it goes around
its elliptical orbit is equal to the length of the semimajor axis. Thus,
by the "radius" of a planet's orbit one usually means the length
of the semimajor axis. For a more detailed investigation of the properties of
ellipses, see this
ellipse applet
3. The long axis of the ellipse is called the major axis, while the
short axis is called the minor axis (adjacent figure). Half of the
major axis is termed a semimajor axis. The
length of a semimajor axis is often termed the size of the ellipse. It can
be shown that the average separation of a planet from the Sun as it goes around
its elliptical orbit is equal to the length of the semimajor axis. Thus,
by the "radius" of a planet's orbit one usually means the length
of the semimajor axis. For a more detailed investigation of the properties of
ellipses, see this
ellipse applet
The Laws of Planetary Motion
Kepler obtained Brahe's data after his death despite the attempts by Brahe's
family to keep the data from him in the hope of monetary gain. There is some
evidence that Kepler obtained the data by less than legal means; it is
fortunate for the development of modern astronomy that he was successful.
Utilizing the voluminous and precise data of Brahe, Kepler
was eventually able to build on the realization that the orbits of the
planets were ellipses to formulate his Three Laws of Planetary
Motion.
Kepler's First Law:
|
I. The orbits of the planets are ellipses, with the Sun at one focus of
the ellipse.
|
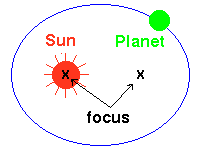 |
Kepler's First Law is illustrated in the image shown above.
The Sun is not at the center of the ellipse, but is instead at one focus
(generally there is nothing at the other focus of the ellipse). The planet
then follows the ellipse in its orbit, which means that the Earth-Sun distance
is constantly changing as the planet goes around its orbit. For purpose of
illustration we have shown the orbit as rather eccentric; remember that the
actual orbits are much less eccentric than
this.
Kepler's Second Law:
|
II. The line joining the planet to the Sun sweeps out equal areas in equal
times as the planet travels around the
ellipse.
|
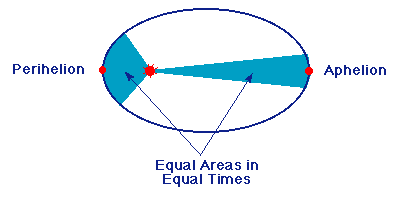 |
Kepler's second law is illustrated in the preceding figure.
The line joining the Sun and planet sweeps out equal areas in
equal times, so the planet moves faster when it is nearer the Sun. Thus,
a planet executes elliptical motion
with constantly changing angular speed as it moves about
its orbit.
The point of nearest approach of the planet to the Sun is termed
perihelion; the point of greatest separation
is termed aphelion. Hence, by Kepler's second law,
the planet moves fastest when it is
near perihelion and slowest when it is near aphelion.
Kepler's Third Law:
|
III. The ratio of the squares of the revolutionary
periods for two planets is equal to
the ratio of the cubes of their semimajor axes:
|
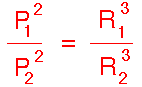 |
In this equation P represents the period of revolution (orbit) for
a planet around the sun and R represents the
length of its semimajor axis. The subscripts "1" and "2" distinguish
quantities for planet 1 and 2 respectively. The periods for the two planets
are assumed to be in the same time units and the lengths of the semimajor axes
for the two planets are assumed to be in the same distance units.
Kepler's Third Law implies that the period for a planet to orbit the Sun increases
rapidly with the radius of its orbit. Thus, we find that Mercury, the innermost
planet, takes only 88 days to orbit the Sun but the outermost planet (Pluto)
requires 248 years to do the same.
Here is a
java applet
allowing you to investigate Kepler's Laws, and
Here is an
animation illustrating the actual relative periods of the inner planets.
Calculations Using Kepler's Third Law
A convenient unit of measurement for periods is in Earth years, and a
convenient unit of measurement for distances is the average separation of the
Earth from the Sun, which is termed an astronomical unit and is
abbreviated as AU.
If these units are used in Kepler's 3rd Law, the denominators in the preceding
equation are numerically equal to unity and it may be written in the simple
form
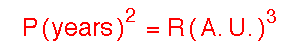
This equation may then be solved for the period P of the
planet, given the length of the semimajor axis,
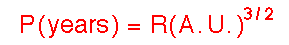
or for the length of the semimajor axis, given the period of the planet,
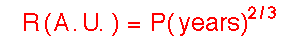
As an example of using Kepler's 3rd Law, let's calculate the "radius" of the
orbit of Mars (that is, the length of the semimajor axis of the orbit) from
the orbital
period. The time for Mars to orbit the Sun is observed to be 1.88 Earth
years. Thus, by Kepler's 3rd Law the length of the semimajor axis for the
Martian orbit is
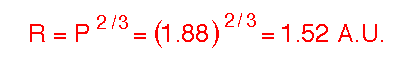
which is exactly the measured average distance of Mars from the Sun.
As a second example, let us calculate the orbital period for Pluto, given that
its observed average separation from the Sun is 39.44 astronomical units.
From Kepler's 3rd
Law
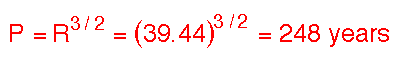
which is indeed the observed orbital period for the planet Pluto.
Supplementary References
 It fell to
Kepler to provide the final piece of the puzzle: after a long struggle, in
which he tried mightily to avoid his eventual conclusion, Kepler was
forced finally to the realization that
the orbits of the planets were not the circles demanded by Aristotle and
assumed implicitly by Copernicus, but were instead
the "flattened circles" that geometers call
ellipses
(See adjacent figure; the planetary orbits are only slightly
elliptical and are not as flattened as in this example.)
It fell to
Kepler to provide the final piece of the puzzle: after a long struggle, in
which he tried mightily to avoid his eventual conclusion, Kepler was
forced finally to the realization that
the orbits of the planets were not the circles demanded by Aristotle and
assumed implicitly by Copernicus, but were instead
the "flattened circles" that geometers call
ellipses
(See adjacent figure; the planetary orbits are only slightly
elliptical and are not as flattened as in this example.)
 Johannes Kepler: The
Johannes Kepler: The Kepler and Brahe did not get along well. Brahe apparently mistrusted Kepler,
fearing that his bright young assistant might eclipse him as the premiere
astonomer of his day. He therefore let Kepler see only part of his voluminous
data.
Kepler and Brahe did not get along well. Brahe apparently mistrusted Kepler,
fearing that his bright young assistant might eclipse him as the premiere
astonomer of his day. He therefore let Kepler see only part of his voluminous
data.
 1. For an ellipse there are
two points called foci (singular: focus) such that the
sum of the distances to the foci from any point on the ellipse is a constant.
In terms of the diagram shown to the left,
with "x" marking the location of the foci, we
have the equation
1. For an ellipse there are
two points called foci (singular: focus) such that the
sum of the distances to the foci from any point on the ellipse is a constant.
In terms of the diagram shown to the left,
with "x" marking the location of the foci, we
have the equation

 3. The long axis of the ellipse is called the major axis, while the
short axis is called the minor axis (adjacent figure). Half of the
major axis is termed a semimajor axis. The
length of a semimajor axis is often termed the size of the ellipse. It can
be shown that the average separation of a planet from the Sun as it goes around
its elliptical orbit is equal to the length of the semimajor axis. Thus,
by the "radius" of a planet's orbit one usually means the length
of the semimajor axis. For a more detailed investigation of the properties of
ellipses, see this
3. The long axis of the ellipse is called the major axis, while the
short axis is called the minor axis (adjacent figure). Half of the
major axis is termed a semimajor axis. The
length of a semimajor axis is often termed the size of the ellipse. It can
be shown that the average separation of a planet from the Sun as it goes around
its elliptical orbit is equal to the length of the semimajor axis. Thus,
by the "radius" of a planet's orbit one usually means the length
of the semimajor axis. For a more detailed investigation of the properties of
ellipses, see this