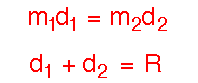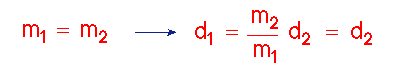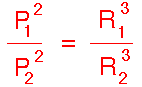Sir Isaac Newton: The
Universal Law of Gravitation
There is a popular story that Newton was sitting under an apple tree, an apple
fell on his head, and he suddenly thought of the Universal Law of Gravitation.
As in all such legends, this is almost certainly not true in its details,
but the story
contains elements of what actually happened.
What Really Happened with the Apple?
Probably the more correct version of the story is that Newton, upon observing
an apple fall from a tree, began to think along the following lines:
The apple is accelerated, since its velocity
changes from zero as it is hanging on the tree and moves toward the ground.
Thus, by Newton's 2nd Law there must be a force that acts on the apple to cause
this acceleration. Let's
call this force "gravity", and the associated acceleration the "acceleration due
to gravity".
Then imagine the apple tree is twice as high. Again,
we expect the apple to be accelerated toward the ground, so this suggests that
this force that we call gravity reaches to the top of the tallest
apple tree.
Sir Isaac's Most Excellent Idea
Now came Newton's truly brilliant
insight: if the force of gravity reaches to the top of the highest tree, might
it not reach even further; in particular, might it not reach all the way
to the orbit of the Moon! Then, the
orbit of the Moon about the Earth could be a consequence of the gravitational
force, because the acceleration due to gravity could change the velocity of the
Moon in just such a way that it followed an orbit
around the earth.
This can be illustrated with the thought experiment shown in the
following figure. Suppose we fire a cannon horizontally from a high mountain;
the projectile will eventually fall to earth, as indicated by the shortest
trajectory in the figure, because of the gravitational
force directed toward the center of the Earth and the associated acceleration.
(Remember that an acceleration is a
change in velocity and that velocity is a vector, so it has both a magnitude
and a direction. Thus, an acceleration occurs if either or both the magnitude
and the direction of the velocity change.)
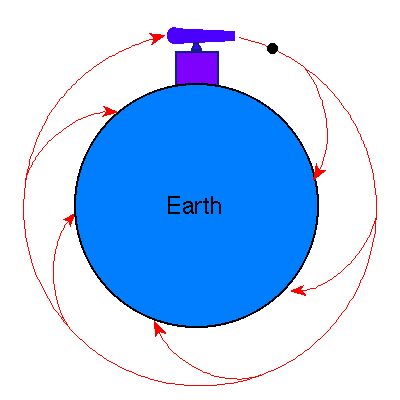
But as we increase the muzzle velocity for our imaginary cannon, the projectile
will travel further and further before returning to earth.
Finally, Newton reasoned that if the cannon projected the cannon ball with
exactly the right velocity, the projectile would travel completely around the
Earth, always falling in the gravitational field but never reaching the Earth,
which is curving away at the same rate that the projectile falls.
That is,
the cannon ball would have
been put into orbit around the Earth.
Newton concluded that the orbit of the
Moon was of exactly the same nature: the Moon continuously "fell" in its path
around the Earth because of the acceleration due to gravity, thus producing its
orbit.
By such reasoning, Newton came to the conclusion that any two objects in the
Universe exert gravitational attraction on each other, with the
force having a universal form:
The constant of proportionality G is known as the universal gravitational
constant. It is termed a "universal constant" because it is thought
to be the same at all
places and all times, and thus universally
characterizes the intrinsic strength of the
gravitational force.
The Center of Mass for a Binary System
If you think about it a moment, it may seem a little strange that in Kepler's
Laws the Sun is fixed at a point in space and the planet revolves around it.
Why is the Sun privileged? Kepler had rather mystical ideas about
the Sun, endowing it with almost god-like qualities that justified its special
place.
However Newton, largely as a corollary of his 3rd Law,
demonstrated that the situation actually was more symmetrical than Kepler
imagined and that the Sun does not occupy a privileged position;
in the process he modified Kepler's 3rd Law.
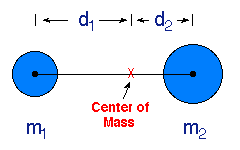Consider the diagram shown to the right.
We may define a point called the center of
mass between two objects through the equations
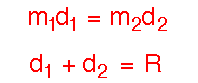
where R is the total separation between the centers of the two objects.
The center of mass is familiar to anyone who has ever played on a see-saw.
The fulcrum
point at which the see-saw will exactly balance two people sitting on
either end is the center of mass for the two persons sitting on the see-saw.
Two Limiting Cases
We can gain further insight by considering the position of the center of mass
in two limits. First consider the example just addressed, where one mass
is much larger than the other. Then, we see that the center of mass for the
system essentially coincides with the center of the massive object:
This is the situation in the Solar System: the Sun is so massive compared with
any of the planets that the center of mass for a Sun-planet pair is always
very near the center of the Sun.
Thus, for all practical purposes the Sun IS almost
(but not quite) motionless at the center of mass for the system, as Kepler
originally thought.
However, now consider the other limiting case where the two masses are equal to
each other.
Then it is easy to see that the center of mass lies equidistant
from the two masses and if they are gravitationally bound to each other,
each mass orbits the common center of mass for the
system lying midway between them:
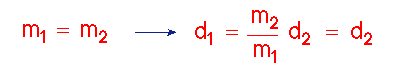
This situation occurs commonly with
binary stars
(two stars bound
gravitationally to each other so that they revolve around their common center
of mass). In many binary star systems the masses of the two stars are similar
and Newton's correction to Kepler's 3rd Law is very large.
These limiting cases for the location of the center of mass
are perhaps familiar from our afore-mentioned playground
experience.
If persons of equal weight are on a see-saw, the fulcrum must be
placed in the middle to balance, but if one person weighs much more than the
other person, the fulcrum must be placed close to the heavier person to
achieve
balance.
Circular Velocity and Geosynchronous Orbit
How fast do we have to travel in a rocket to stay in circular
orbit around a much more massive body such as the Earth?
I will present the answer without derivation here, but it follows from
Newton's law of gravitation.
If we assume that the mass of the rocket is small compared to the Earth,
then the CIRCULAR VELOCITY is given by the square root of GM/r, that is
Vcirc = (GM/R)1/2
where G is the gravitational constant,
R is the radius of the orbit, M is the mass of the larger object,
like the Earth, around which the smaller object orbits.
Note that the formula does not depend on the mass of the smaller object.
(This last fact follows from the Newtonian theory, and is
related to the experimental inference by Galileo that
two objects of different mass dropped from the same height
fall to Earth in the same time.)
We can use this formula to calculate how fast the moon moves in
its orbit around the Earth. Plugging in the Earth's mass of
M=6 x 1024 kg,
the radius of the moon's orbit of R=3.84 x 108 meters,
and gravitational constant G= 6.67 x 10-11
Newton meter2 / kg2,
the magnitude of the moon's velocity is then 1020 meter/s. This is about 2278 miles per hour.
(Hey so if its moving so fast, 5 times faster
than jet airplanes, why do jets seem to move faster on the sky than the moon?
You'll have to answer this question on your own..)
Since the circular velocity varies inversely with the square root of R,
an object in a smaller
orbit has faster speed because the gravity is stronger.
The same calculation for R=6578 km above the center of the
Earth tells us that a satellite must move at speeds of 17,400 miles
per hour (=7790 m/s). Thus rockets have to move incredibly fast.
The rocket has to get up, and then turn to point in a circular
orbit at the correct speed. But once it is at that speed, it will
stay in orbit without subsequent rocket propulsion.
Since the orbital velocity of a satellite depends on its distance
from the center of the Earth, the farther out, the longer the period
of the orbit. Near the Earth the orbital period is about 1.5 hours.
If one goes out to about 42,000 km (26,000) miles, the orbital period
is 24 hours. Thus the satellite would be in GEOSYNCHRONOUS ORBIT.
Imagine launching a satellite eastward above the Earth's equator
in geosynchronous orbit: then the satellite will stay over the same spot
on the Earth at all times in its orbit.
Open and Closed Orbits
Orbits which close on themselves like circular or elliptical
orbits are called CLOSED ORBITS.
The object in such orbits always return to the same place in the orbit
periodically. In circular orbits, the speed of the object remains
the same everywhere in the orbit. In elliptical orbits the speed
is faster as the object moves to the closer part of its orbit and
then slows as the object proceeds to the farther part of the orbit.
There are also orbits called ESCAPE ORBITS or OPEN ORBITS.
In these orbits the object never returns and goes off to large
distances.
To see this
Imagine a cannon shooting off of a mountain on the surface
of the Earth (fig 5-13).
There are 5 qualitatively different possibilities depending on how fast the cannonball
travels with respect to the circular velocity initially.
If it travels at the circular velocity, the orbit will be circular.
If it travels much less than circular velocity the cannon ball will
drop to the surface.
If it travels a little bit less than circular velocity,
it will form an elliptical orbit with the cannon
at APOGEE (the farthest point in the orbit).
If the ball travels a little bit faster than circular velocity, then
it will form an elliptical orbit with the cannon at the PERIGEE (the
nearest point in the orbit).
If the ball travels at the ESCAPE VELOCITY (see below), then
the orbit will be OPEN and will be a parabola.
If the ball travels faster than the ESCAPE VELOCITY,
the orbit with be OPEN and be a hyperbola.
Escape Velocity
The ESCAPE VELOCITY from an object like the Earth is given by
Ves = (2GM/R)1/2
where R is the radius of the launch point for the object.
When the launch point is on the Earth's surface, then
R would be the radius of the Earth.
This escape velocity is the critical velocity an object must have
to subsequently coast to infinity when shot upward from within
a gravitational field. That is, if a rocket is shot from the Earth and
consumes all of its fuel to accelerate to this velocity, then even
after the rocket is no longer burning fuel, it will coast
to infinity and the Earth's gravity cannot pull the rocket back to
Earth.
Plugging in for the Earth's mass, radius, and for G,
we obtain 11.2 km/s for the escape velocity for an object launched
from the Earth's surface. This is about 25,000 miles per hour!
I dare you to try to escape. (So much for Aristotle's worries about
birds flying off the Earth's surface-- no chance in the presence of gravity.)
Weight and the Gravitational Force
We have seen that in the Universal Law of Gravitation the crucial quantity is
mass. In popular language mass and weight are often used to mean the same
thing; in reality they are related but quite different things. What we
commonly call weight is really just the
gravitational force
exerted on an
object of a certain mass. We can illustrate by choosing
the Earth as one of the two masses
in the previous illustration of the Law of Gravitation:
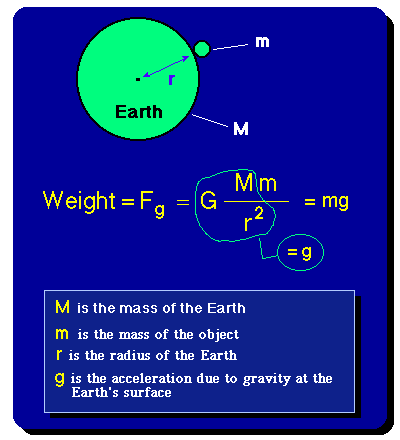
Thus, the weight of an object of mass m at the surface of the Earth is obtained
by multiplying the mass m by the acceleration due to gravity,
g, at the surface
of the Earth. The acceleration due to gravity is approximately the product of
the universal gravitational constant G and the mass of the Earth
M,
divided by the radius of the Earth, r, squared.
(We assume the Earth to be
spherical and neglect the radius of the object relative to the radius of the
Earth in this discussion.) The measured gravitational acceleration at the
Earth's surface is found to be about 9.8 m/second2.
Mass and Weight
Mass is a measure of how much material is in an object, but
weight is a measure of
the gravitational force exerted on that material in a gravitational field;
thus, mass and weight are proportional to each other, with the acceleration due
to gravity as the proportionality constant.
It follows that
mass is constant for an object (actually this is not quite true, but we
will save that surprise for our later discussion of the
Relativity Theory),
but weight depends on the location of the object.
For example, if we transported the preceding object of mass
m to the surface of
the moon, the gravitational acceleration would change because the radius and
mass of the Moon both differ from those of the Earth. Thus, our object
has mass m
both on the surface of the Earth and on the surface of the Moon, but it
will weigh much less on the surface of the Moon
because the gravitational acceleration there is a factor of 6
less than at the surface
of the Earth.
Newton's Derivation of Kepler's Laws
Notice that magnitude of the circular velocity of an object in orbit
is also equal to the
the circumference of an orbit divided by the period of the orbit.
That is:
Vcirc = (GM/R)1/2 = (2 pi R)/ P
where pi=3.1415 and P is the orbital period.
The latter equality follows from simply noting that the magnitude
of velocity is a measurement of distance traveled per unit time.
The distance traveled is the circumference of the orbit (= 2 pi R),
and the period P is the time it takes to travel this distance.
But look: now magically we have recovered Kepler's third law!:
Rearranging the latter equality we have
(GM) P2 = 4 pi2 R3
the point being that P2 is proportional to R3. That is Kepler's 3rd
law, now falling directly from Newton's theory.
Newton's Interpretation of Kepler's Laws
Because for every action there is an equal
and opposite reaction, Newton realized that in the planet-Sun system the planet
does not orbit around a stationary Sun. Instead, Newton proposed that both the
planet and the Sun orbited around the common center of mass for the planet-Sun
system. He then modified Kepler's 3rd Law so that the mass
M used is now the sum of the mass of the Sun plus the planet.
Instead of using M1 and M2 as above, let us use Ms and Mp. Then we
have M= Ms + Mp and so
G(Ms + Mp
) P
2 = 4 pi2 R3
But notice what happens in Newton's new equation if the mass
of the sun is much larger than the mass for any of the planets
(which is always the case).
Then the sum of the two masses is always approximately equal to the mass of the
Sun and so are back to
G Ms P2 = 4 pi2 R3
for planet-Sun systems.
If we take ratios of Kepler's 3rd Law for two different planets the Sun mass
then cancels from the ratio and we are left with the
original form of Kepler's 3rd Law:
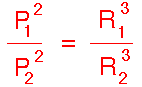
Thus Kepler's 3rd Law is approximately valid because the Sun is much more
massive than any of the planets and therefore
Newton's correction is small. The data Kepler had access to were not good
enough to show this small effect. However,
detailed observations made after Kepler show that Newton's modified form of
Kepler's 3rd Law is in better accord with the data than Kepler's original form.
