 Newtonian Gravitation and the
Newtonian Gravitation and the
Laws of Kepler
We now come to the great synthesis of dynamics and astronomy accomplished by
Newton: the Laws of Kepler for planetary motion may be derived from Newton's
Law of Gravitation. Furthermore, Newton's Laws provide corrections to Kepler's
Laws that turn out to be observable, and Newton's Law of Gravitation will be
found to describe the motions of all objects in the heavens, not just the
planets.
Acceleration in Keplerian Orbits
Kepler's Laws are illustrated in the adjacent animation. The red arrow
indicates the instantaneous velocity vector at each point on the orbit
(as always, we greatly exaggerate the eccentricty of the ellipse for purposes
of illustration). Since the velocity is a vector, the direction of the
velocity vector is indicated by the direction of the arrow and the magnitude
of the velocity is indicated by the length of the arrow.
Notice that (because
of Kepler's 2nd Law) the velocity vector is constantly changing both its
magnitude and its direction as it moves around the elliptical
orbit (if the orbit were circular, the magnitude of the velocity would remain
constant but the direction would change continuously). Since either a
change in the magnitude or the direction of the velocity vector constitutes an
acceleration, there is a continuous acceleration as the
planet moves about its orbit (whether circular or elliptical),
and therefore by Newton's 2nd Law there is a force that acts at every
point on the orbit. Furthermore, the force is not constant in
magnitude, since the change
in velocity (acceleration) is larger when the planet is near the Sun on the
elliptical orbit.
Newton's Laws and Kepler's Laws
Since this is a survey course, we shall not cover all the mathematics, but we
now outline how Kepler's Laws are implied by those of
Newton, and use Newton's Laws to supply corrections to Kepler's Laws.
- Since the planets move on ellipses
(Kepler's 1st Law), they are continually accelerating, as
we have noted above. As we have also noted above, this implies a force acting
continuously on the planets.
- Because the planet-Sun line sweeps out equal areas in equal times
(Kepler's 2nd Law), it is possible to show that the force must be directed
toward the Sun from the planet.
- From Kepler's 1st Law the orbit is an ellipse with the Sun at one focus;
from Newton's laws
it can be shown that this means that the magnitude of the force must vary as
one over the square of the distance between the planet and the Sun.
- Kepler's 3rd Law and Newton's 3rd Law imply that the
force must be proportional to the product of the masses for the planet and the
Sun.
Thus, Kepler's laws and Newton's laws taken together imply that the force that
holds the planets in their orbits by continuously changing the planet's
velocity so that it follows an elliptical path is
(1) directed toward the Sun from the
planet, (2)
is proportional to the product of masses for the Sun and planet, and
(3) is
inversely proportional to the square of the planet-Sun separation. This is
precisely the form of the
gravitational force, with the universal
gravitational constant G as the constant of proportionality. Thus,
Newton's laws of motion, with a gravitational force used in the 2nd Law, imply
Kepler's Laws, and the planets obey the same laws of motion as objects
on the surface of the Earth!
Conic Sections and Gravitational Orbits
As mentioned the ellipse is not the only possible orbit in a
gravitational field. According to Newton's analysis, the
possible orbits in a gravitational field can take the shape of the figures
that are known as conic sections (so called because they
may be obtained by slicing sections from a cone, as illustrated in the
following figure).
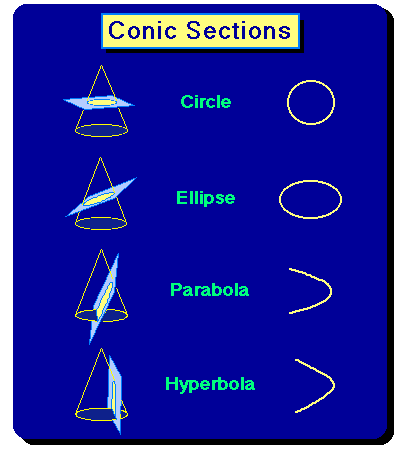
For the ellipse (and its special case, the circle),
the plane intersects opposite "edges" of the cone.
For the parabola the plane is parallel to one edge of the cone; for the
hyperbola the plane is not parallel to an edge but it does not
intersect opposite "edges" of the cone.
(Remember that these cones extend forever downward; we have shown them with
bottoms because we are only displaying a portion of the cone.)
Examples of Gravitational Orbits
We see examples of all these possible orbitals in gravitational fields. In
each case, the determining factor influencing the nature of the orbit is the
relative speed of the object in its orbit as discussed above.

- The orbits of some of the planets (e.g., Venus) are ellipses of such small
eccentricity that they are essentially circles, and we can put artificial
satellites into orbit around the Earth with circular orbits if we choose.
- The orbits of the planets generally are ellipses.
- Some comets have parabolic orbits; this means that they pass the Sun once
and then leave the Solar System, never to return. Other comets have elliptical
orbits and thus orbit the Sun with specific periods.
- The gravitational interaction between two passing stars generally results
in hyperbolic trajectories for the two stars.
Thus, Kepler's elliptical orbitals are but one example of the possible
orbits in a gravitational field. Only ellipses (and their special case, the
circle) lead to bound orbits; the others are associated with one-time
gravitational encounters.
Here is a set of Java applets, taken from the
Famous Curves Applet Index
that illustrate the geometrical properties of these gravitational orbits:
-
Java applet illustrating properties of a circle
-
Java applet illustrating properties of an ellipse
-
Java applet illustrating properties of an hyperbola
-
Java applet illustrating properties of a parabola
For a given central force, increasing the velocity causes the orbit to change
from a circle to an ellipse to a parabola to a hyperbola, with the changes
occurring at certain critical velocities. For example, if the speed of
the Earth (which is in a nearly
circular gravitational orbit) were
increased by about a factor of 1.4, the orbit would change into a parabola and
the Earth would leave the Solar System.

 Newtonian Gravitation and the
Newtonian Gravitation and the

