Laws

|
Radiation Laws |
To understand the light we see from stars, we have to understand how photons are produced, and how the TEMPERATURE (a measure of the average velocity of particles in a material) is related to atomic motions. The second issue is straightforward. The faster the average motions of atoms the higher the temperature. Hotter materials have faster moving atoms.
To address the first issue note that light is produced by a changing electromagnetic field. If we disturb the motion of a charged particle like an electron, the sudden change in the electric field around it produces an electromagnetic wave. If you run a comb through your hair, you disturb the electrons in the comb and your hair and produce an electromagnetic waves. If you turn on an AM radio, you will hear pops: the wave has propagated from your hair to the radio. This is the same with an astronomical object: changes in electron motions produce electromagnetic waves which propagate and this is the light that we observe.
Thus we can immediately realize that hotter objects emit more radiation: the hotter the object, the more atomic motions disturb electrons and the more radiation that is emitted.
The radiation emitted by a heated object is called BLACKBODY radiation. It refers to the fact that at room temperature, a perfect emitter is also a perfect absorber and would look black. This is because all radiation coming into the object is absorbed and then re-radiated so you see no net emission from the object. If the object is at higher than room temperature it would glow.
As long as the temperature of an object is larger than ABSOLUTE ZERO (on the Kelvin scale) the atoms have thermal energy and can radiate. Thus ice cubes radiate some photons.
The average or bulk properties of electromagnetic radiation interacting with matter are systematized in a simple set of radiation laws. These laws apply when the radiating body is a blackbody radiator. This means that it is not interacting very much with its surrounding environment and is more or less at equilibrium. Although stars do not satisfy perfectly the conditions to be blackbody radiators, they do to a sufficiently good approximation that it is useful to view stars as approximate blackbody radiators.
The Wien and Stefan-Boltzmann Laws
The behavior of blackbody radiation is described by the Planck Law, but we can
derive from the Planck Law two other radiation laws that are very useful. The
Wien Displacement Law, and the Stefan-Boltzmann Law are illustrated in the
following equations.
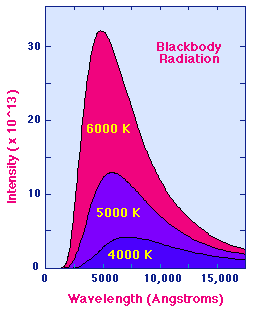
The Wien Law gives the wavelength of the peak of the radiation distribution,
while the Stefan-Boltzmann Law gives the total energy being emitted at all
wavelengths by the blackbody (which is the area under the Planck Law curve).
Thus, the Wien Law explains the shift of the peak to shorter wavelengths as the
temperature increases, while
the Stefan-Boltzmann Law explains the growth in the
height of the curve as the temperature increases. Notice that this growth is
very abrupt, since it varies as the fourth power of the temperature.
| Some Blackbody Temperatures | |||
|---|---|---|---|
| Region | Wavelength (centimeters) |
Energy (eV) |
Blackbody Temperature (K) |
| Radio | > 10 | < 10-5 | < 0.03 |
| Microwave | 10 - 0.01 | 10-5 - 0.01 | 0.03 - 30 |
| Infrared | 0.01 - 7 x 10-5 | 0.01 - 2 | 30 - 4100 |
| Visible | 7 x 10-5 - 4 x 10-5 | 2 - 3 | 4100 - 7300 |
| Ultraviolet | 4 x 10-5 - 10-7 | 3 - 103 | 7300 - 3 x 106 |
| X-Rays | 10-7 - 10-9 | 103 - 105 | 3 x 106 - 3 x 108 |
| Gamma Rays | < 10-9 | > 105 | > 3 x 108 |
Blackbody radiation corresponds to radiation from bodies in thermal equilibrium. We will consider later the emission of non-thermal radiation, which doesn't follow a blackbody law. Such radiation is often produced by violent collisions rather than equilibrium heating. For example, in astrophysical environments radiation at the long and short wavelength ends of the above table is more likely to be produced by non-thermal processes.
Here are three Java applets illustrating some important properties of blackbody radiation.
You may use these virtual experiments to gain some experience with how Planck distributions evolve with temperature.