 |
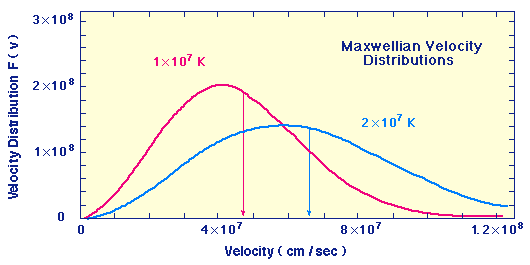
| Maxwellian Velocity Distributions for Two Temperatures |
| Temperature and Pressure in Stars |
Stars are composed of hot gases in which the atoms and molecules are almost completely ionized in the interior (the state of matter called a plasma). The question of whether fusion reactions can occur in this plasma is primarily one of the density and the temperature of the gas, because the density controls the number of collisions and the temperature controls their average energy. Since for a fixed volume and temperature the density and pressure are directly related, we may also use the pressure instead of the density as a variable.
 |
| Maxwellian Velocity Distributions for Two Temperatures |
In this plot the horizontal axis is the velocity in cm/sec and the vertical axis is proportional to the probability that a particle in the gas has that velocity.
Thus, we see that each temperature corresponds to a range of velocities, but the average velocity (indicated by the vertical lines) increases with temperature, and likewise the probability of having very high velocities for some gas particles increases with temperature.
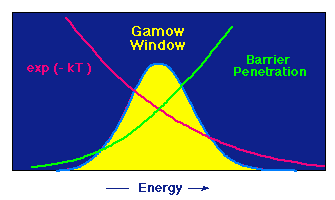 |
| The Gamow window for charged-particle reactions |
The peak is the product of the two curves decreasing in opposite directions: The probablility for penetrating the Coulomb barrier goes down rapidly with decreasing energy (the curve marked "barrier penetration"), but at a given temperature the possibility of having a particle of high energy (and therefore high velocity) decreases rapidly with increasing energy (the red curve).
The sum of these opposing effects produces an energy window for the nuclear reaction: only if the particles have energies approximately in this window can the reaction take place. This places very strong constraints on the charged-particle reactions responsible for producing fusion energy in stars.