Vectors: Velocities,
Accelerations, and Forces

In order to understand the discoveries of Newton, we must have an understanding of three basic quantities: (1) velocity, (2) acceleration, and (3) force. In this section we define the first two, and in the next we shall introduce forces. These three quantities have a common feature: they are what mathematicians call vectors.

Examples of Scalar Quantities

Vectors are quantities that require not only a magnitude, but a direction to specify them completely. Let us illustrate by first citing some examples of quantities that are not vectors. The number of gallons of gasoline in the fuel tank of your car is an example of a quantitity that can be specified by a single number---it makes no sense to talk about a "direction" associated with the amount of gasoline in a tank. Such quantities, which can be specified by giving a single number (in appropriate units), are called scalars. Other examples of scalar quantities include the temperature, your weight, or the population of a country; these are scalars because they are completely defined by a single number (with appropriate units).

Examples of Vector Quantities

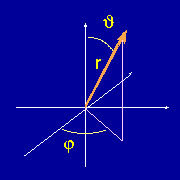However, consider a velocity. If we say that a car is going 70 km/hour, we have not completely specified its motion, because we have not specified the direction that it is going. Thus, velocity is an example of a vector quantity. A vector generally requires more than one number to specify it; in this example we could give the magnitude of the velocity (70km/hour), a compass heading to specify the direction (say 30 degrees from North), and an number giving the vertical angle with respect to the Earth's surface (zero degrees except in chase scenes from action movies!). The adjacent figure shows a typical coordinate system for specifying a vector in terms of a length r and two angles, theta and phi.

Graphical Representation of Vectors

Vectors are often distinguished from scalar quantities either by placing a small arrow over the quantity, or by writing the quantitity in a bold font. It is also common to indicate a vector by drawing an arrow whose length is proportional to the magnitude of the vector, and whose direction specifies the orientation of the vector.

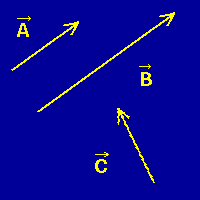
In the adjacent image we show graphical representations for three vectors. Vectors A and C have the same magnitude but different directions. Vector B has the same orientation as vector A, but has a magnitude that is twice as large. Each of these represents a different vector, because for two vectors to be equivalent they must have both the same magnitudes and the same orientations.

Velocity and Acceleration

Let us now give a precise definition of velocity and acceleration. They are vectors, so we must give a magnitude and a direction for them. The velocity v and the acceleration a are defined in the following illustration,

This illustration also demonstrates graphically that velocity (and therefore acceleration) is a vector: the direction of the rock's velocity is certainly of critical interest to the person standing under the rock in the two illustrations!

Uniform Circular Motion is Accelerated Motion

 Notice that velocity, which is a vector, is changed if either its magnitude or its direction is changed. Thus, acceleration occurs when either the magnitude or direction of the velocity (or both) are altered.

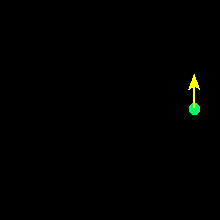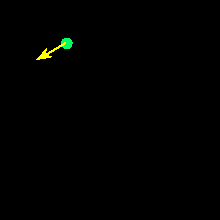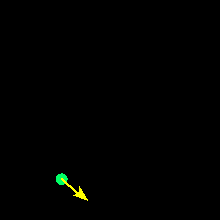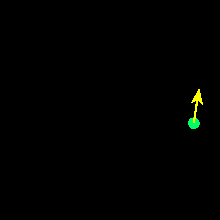
In particular, notice from the adjacent image that circular motion (even at uniform angular velocity) implies a continual acceleration, because the direction of the velocity (indicated by the direction of the arrow) is continuously changing, even if its magnitude (indicated by the length of the arrow) is constant. This point, that motion on a curved path is accelerated motion, will prove crucial to our subsequent understanding of motion in gravitational fields.

How Many Accelerators Does Your Car Have?

Be aware that in popular speech acceleration is assumed to be an increase in the magnitude of the velocity. As we have just seen, acceleration also occurs when the direction of the velocity is changed, even if the magnitude is constant; furthermore, in physics a decrease in the velocity is just as much an acceleration as a decrease. Thus, your car actually has at least 3 accelerators: (1) the foot pedal called the "accelerator", that changes the magnitude of the velocity, (2) the brake, which also changes the magnitude of the velocity, and (3) the steering wheel, which changes the direction of the velocity!