of Light

| Wave Properties of Light |
In modern physics, light or electromagnetic radiation may be viewed in one of two complementary ways: as a wave in an abstract electromagnetic field, or as a stream of massless particles called photons. Although either is an acceptable description of light, for our purposes in introductory astronomy the wave description will be more useful.
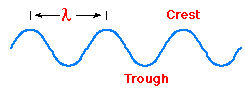 The quantity that is "waving" is the
electromagnetic field, an esoteric but quite measurable entity: your lights
shine and your microwave runs and your radio plays because the electromagnetic
field exists. As
illustrated in the adjacent image, a wave has a wavelength associated with it.
The quantity that is "waving" is the
electromagnetic field, an esoteric but quite measurable entity: your lights
shine and your microwave runs and your radio plays because the electromagnetic
field exists. As
illustrated in the adjacent image, a wave has a wavelength associated with it.
It is normal to give the wavelength of light the symbol Greek "lambda". Some common units of length employed for wavelengths of electromagnetic radiation are summarized in the following table. (The micrometer is often still called by its old name, the micron.)
| Units of Wavelength | ||
|---|---|---|
| Unit | Symbol | Length |
| centimeter | cm | 10-2 meters |
| Angstrom | 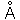 |
10-8 centimeters |
| nanometer | nm | 10-9 meters |
| micrometer | nm | 10-6 meters |
The speed of light in a medium is generally less than this. Normally the term "speed of light", without further qualification, refers to the speed in a vacuum.
A wave can be characterized by its wavelength, but we can also characterize it by the frequency (how many wavelengths pass a fixed point in a given time; think of sitting on the dock---of the bay---counting the number of water waves passing in one minute) and the energy that it carries (think of a water wave knocking you over in heavy surf). For light waves the relationship among the wavelength (usually denoted by Greek "lambda"), the frequency (usually denoted by Greek "nu"), and the energy E are
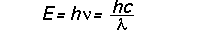
in two different useful sets of units (eV stands for "electron volts"; electron volts and ergs are two common units of energy). Thus, these equations allow us to freely inter-convert among frequency, wavelength, and energy for electromagnetic waves: specifying one also specifies the others.
Radio waves have wavelengths from a few millimeters (microwaves) to kilometers. The wavelength of visible light is short. Visible light ranges from about 4 x 10-7 to 7 x 10-7 meters or 400-700 nm. Often different astronomers from different fields use different units to describe the same phenomena. (Do not confuse the physical concepts with the choice of units.)
Thus another way to think of the above formula for the energy of electromagnetic radiation is to say that it describes the relation between a photon's energy and its wavelength.