 |
| The Zeeman Effect |
| The Zeeman Effect |
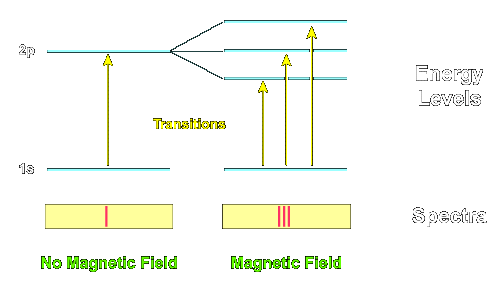
The atomic energy levels, the transitions between these levels, and the associated spectral lines discussed to this point have implicitly assumed that there are no magnetic fields influencing the atom. If there are magnetic fields present, the atomic energy levels are split into a larger number of levels and the spectral lines are also split. This splitting is called the Zeeman Effect.
 |
| The Zeeman Effect |
Atomic physicists use the abbreviation "s" for a level with L=0, "p" for L=1, and "d" for L=2, and so on (the reasons for these designations are of historical interest only). It is also common to precede this designation with the integer principle quantum number n. Thus, the designation "2p" means a level that has n=2 and L=1.
In the preceding example the lowest level is an "s" level, so it has L=0 and 2L + 1 = 1, so it isn't split in the magnetic field, while the first excited state has L=1 ("p" level), so it is split into 2L + 1 = 3 levels by the magnetic field. Thus, a single transition is split into 3 transitions by the magnetic field in this example.
The Zeeman effect can be interpreted in terms of the precession of the orbital angular momentum vector in the magnetic field, similar to the precession of the axis of a spinning top in a gravitational field.
One practical example in astronomy of such polarization effects is that in the preceding example the middle transition is polarized such that it cannot be easily be obverved from directly over a surface perpendicular to the magnetic field. As a consequence, when looking directly down on a sunspot (which have strong magnetic fields) typically only two of the three transitions shown above can be seen and the line is observed to split into two rather than three lines (the missing transition could be observed from a different angle where its light would not be suppressed by the polarization effect, but it is very weak when observed from directly overhead).