Experiments with Electrons and
Neutrinos Reveal Complex Spatial Distribution of Charge and
Magnetization Inside Protons and Neutrons
April 20, 2007: An
analysis by University of Rochester physicists of electron and neutrino
scattering data on protons and neutrons shows a complex spatial charge
and magnetization structure of the proton and neutron. The new
analysis incorporates the effects of the quark structure of the proton
on neutron on their charge distribution. The neutron consists of
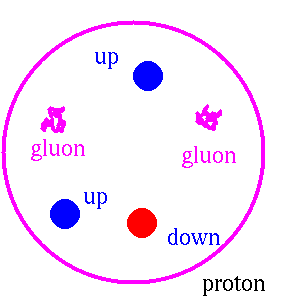
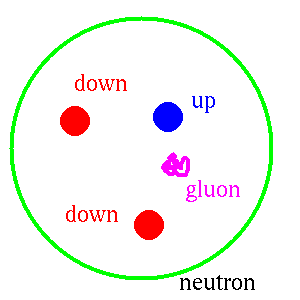
a positively charged up-quark in the center surrounded by two
negatively charged down-quarks on the outside. For the proton, it is
reversed, and the distribution of positively charged up-quarks extends
to larger radius than the distribution of negatively charged
down-quarks. The spatial distribution of electric-magnetization
in the proton and neutron seen in electron scattering is different from
the weak (axial)-magnetization observed in neutrino experiments.

Bodek
|

Avvakumov
|

Bradford
|

Budd
|
Arie Bodek, George E. Pake Professor of Physics and Chair of the
Department of Physics and Astronomy at the University of Rochester, Dr.
Sergei Avvakumov, Dr. Robert Bradford, and Dr. Howard Budd, have worked
on an updated description of the distribution of electric charge,
electric-magnetization, and weak (axial) magnetization inside protons
and neutrons. The new analysis incorporates the effects of the quark
structure of the proton on neutron on their charge distribution.
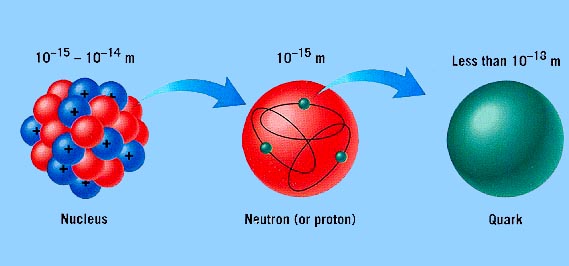
Protons and neutron are composed of quarks bound together by the strong
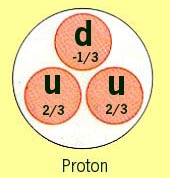
color force. The proton is composed of two positively charged up-quarks
(charge +2/3e) and one negatively charged down-quark (charge -1/3e).
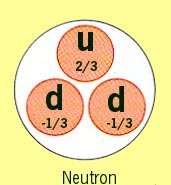
The neutron is composed of two negatively charged down-quarks (charge
-1/3e), and one positively charged up-quark (with charge +2/3e). Within
the quark model, the proton and neutron are mirror images of one
another. This is referred to as isospin symmetry. A neutron can be
considered to be the same as a proton with every down-quarks replaced
with an up-quark and every up-quark replaced with a down-quark
(typically referred to as isospin symmetry) The motion of quarks inside
protons and neutrons results in a spatial distribution electric-charge,
electromagnetic-magnetization and weak (axial)-magnetization inside
protons and neutrons (commonly referred to as nucleons).
Because electrons have a spin, they are small electricallycharged
magnets. Therefore, electrons are scattered by both the
electric-charge and the magnetization inside nucleons.Elastic
scattering of high-energy electron beams from targets composed of
hydrogen and deuterium enable researchers at Jefferson Laboratory to
measure how electric-charge and electric-magnetization are distributed
in the space inside protons and neutrons. Elastic scattering
experiments involve collisions in which after the scattering there is
only a single intact proton in the final state. Similar
experiments with beams of neutrinos and antineutrinos (which scatter
via the weak-force) provide information on the space distribution of
the weak (axial)-magnetization inside protons and neutrons.
In contrast, inelastic scattering experiments involve energetic
collisions of electrons (or neutrinos) with the quarks inside protons
and neutrons, and after the scattering, leave a final state with many
additional particles. Inelastic scattering experiments are used
to measure the momentum (and energy) distribution of quarks inside
protons and neutrons.
The Rochester researchers report on a new analysis of all neutrino
scattering experiments on deuterium to obtain the most precise
determination of the distribution of the weak (axial)-magnetization
inside nucleons. They have also done a global analysis of data from all
elastic electron scattering experiments using theoretical concept
called "duality". Duality relates the spatial distribution of the
quarks to their momentum (and energy) distribution inside nucleons.
Their work focused on determining in precise detail the electric,
magnetic and axial form-factors of the proton and neutron (from which
the space distributions of electric-charge and the two kinds of
magnetization can be extracted). By using these "duality"
relations, they obtain a more precise description of the electric
charge electric-magnetization and weak-magnetization distributions
inside protons and neutrons.
They find that the space distributions of electric-charge,
electric-magnetization, and weak (axial) magnetization are all
different. The electron scattering data on the behavior of the electric
form-factor of the neutron indicates that the neutron, which is
electrically neutral, has an inner core which is positively charged
(composed of one up-quark) surrounded by an outside shell which is
negatively charged (composed of two down-quarks). By isospin symmetry,
the proton is the same as a neutron, with the up and down quarks
reversed. The fact that the up-quark and down-quark distribution
are different in the proton, is confirmed by the data on the electric
form-factor of the proton. It is found that for the proton, the
up-quark (charge +2/3e) distribution extends to larger radius than the
distribution of down-quarks (charge -1/3e).
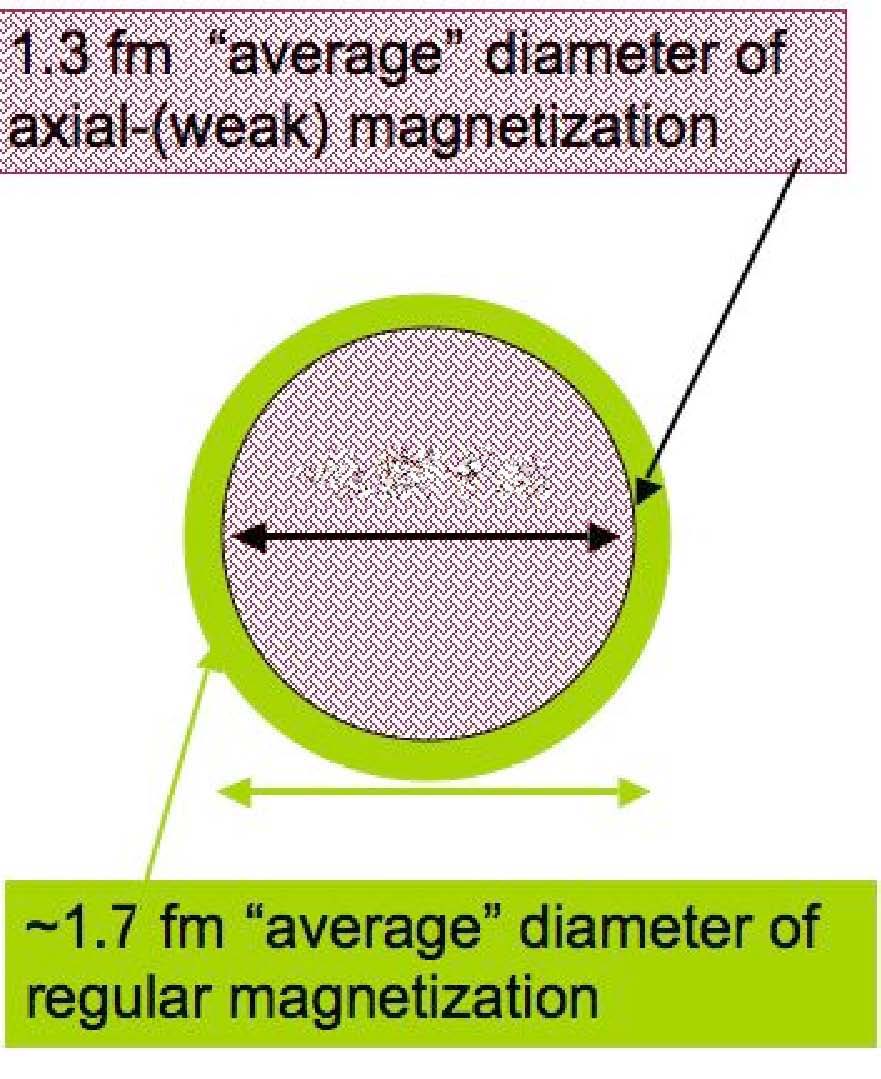
The data on the magnetic form-factors indicates that the
electric-magnetization distribution follows an exponential with an
average radius of about 0.85 Fermi (a Fermi is 10-15 meters) in both
neutrons and protons. The data on the axial-form factor indicates
that the axial (weak) magnetization also follows an exponential with a
smaller average radius of about 0.65 Fermi (for both neutrons and
protons). The measurement of the axial-magnetization with
neutrino beams involves collisions in which up-quarks are changed into
down-quarks and down-quarks are changed into up-quarks.
The elastic scattering experimental data that was used in this analysis
came from measurements done in various laboratories in the USA, Europe
and Japan. The electron scattering data comes primarily from
experiments at the Jefferson Laboratory and the Stanford Linear
Accelerator Center. The neutrino scattering data is from Fermi National
Accelerator Laboratory Brookhaven National Laboratory, and the CERN
complex in Geneva Switzerland.
The more precise extraction of the axial-form factor is also used for
improved modeling of the scattering of neutrinos from neutrons and
protons. These improvements are essential for the new growing field of
neutrino oscillations. Recently, researchers have discovered that
neutrinos oscillate from one type to another. Neutrino oscillations
experiments are done by investigating the collisions of neutrinos with
protons and neutrons as a function of distance from the neutrino
source. The phenomenon of neutrino oscillations was discovered by
investigating the interactions of neutrinos (which are produced by
cosmic rays in the upper atmosphere) in the massive Super-Kamiokande
neutrino detector in Japan. In order to further study this
phenomenon, researchers in Japan have embarked on the construction of a
new accelerator (JPARC) that will produce very intense beams of
low-energy neutrinos for the next generation neutrino oscillations
experiments. US Physicists are also planning to build a next generation
neutrino oscillations detector called Nova that will use the new high
intensity low energy NUMI neutrino beam at Fermilab.
Reliable models of how low energy neutrinos interact with nucleons are
required if these next generation of precise neutrino oscillations
experiments are to achieve their goals.
The University of Rochester researchers who have done this analysis are
also involved the construction of the new MINERvA neutrino
detector at Fermilab. This low energy neutrino experiment will provide
much improved new precise data on the axial form-factor of the nucleon.

MINERvA Detector Design
|
Better and more precise understanding of the structure of the nucleon
provide the basis for all current and future experiments in High Energy
Particle Physics. Professor Bodek was awarded the 2004 APS W.KH.
Panofsky Prize in Experimental Particle Physics "For his broad,
sustained, and insightful contributions to elucidating the structure of
the nucleon, using a wide variety of probes, tools and methods at many
laboratories." This research is part of Bodek's continuing research in
the area of nucleon structure.
Additional Details
For further details, see:
Sergei Avvakumov , Arie Bodek, Robert Bradford and Howard Budd
“Duality Constrained Parameterization
of Vector and Axial Nucleon Elastic Form Factors”
For more information, please contact:
Professor Arie Bodek (University of Rochester)
Faculty Web Page
http://spider.pas.rochester.edu/mainFrame/people/pages_old/Bodek.html
Email: bodek@pas.rochester.edu
Scientist Sergei Avvakumov (University of Rochester)
Email: avva@fnal.gov
Research Associate Robert K. Bradford (University of Rochester)
Web page
http://www.pas.rochester.edu/~bradford/
Email: bradford@pas.rochester.edu
Senior Scientist Howard Budd (University of Rochester)
Web Page
http://spider.pas.rochester.edu/mainFrame/people/pages_old/Budd.html
Email: hbudd@fnal.gov
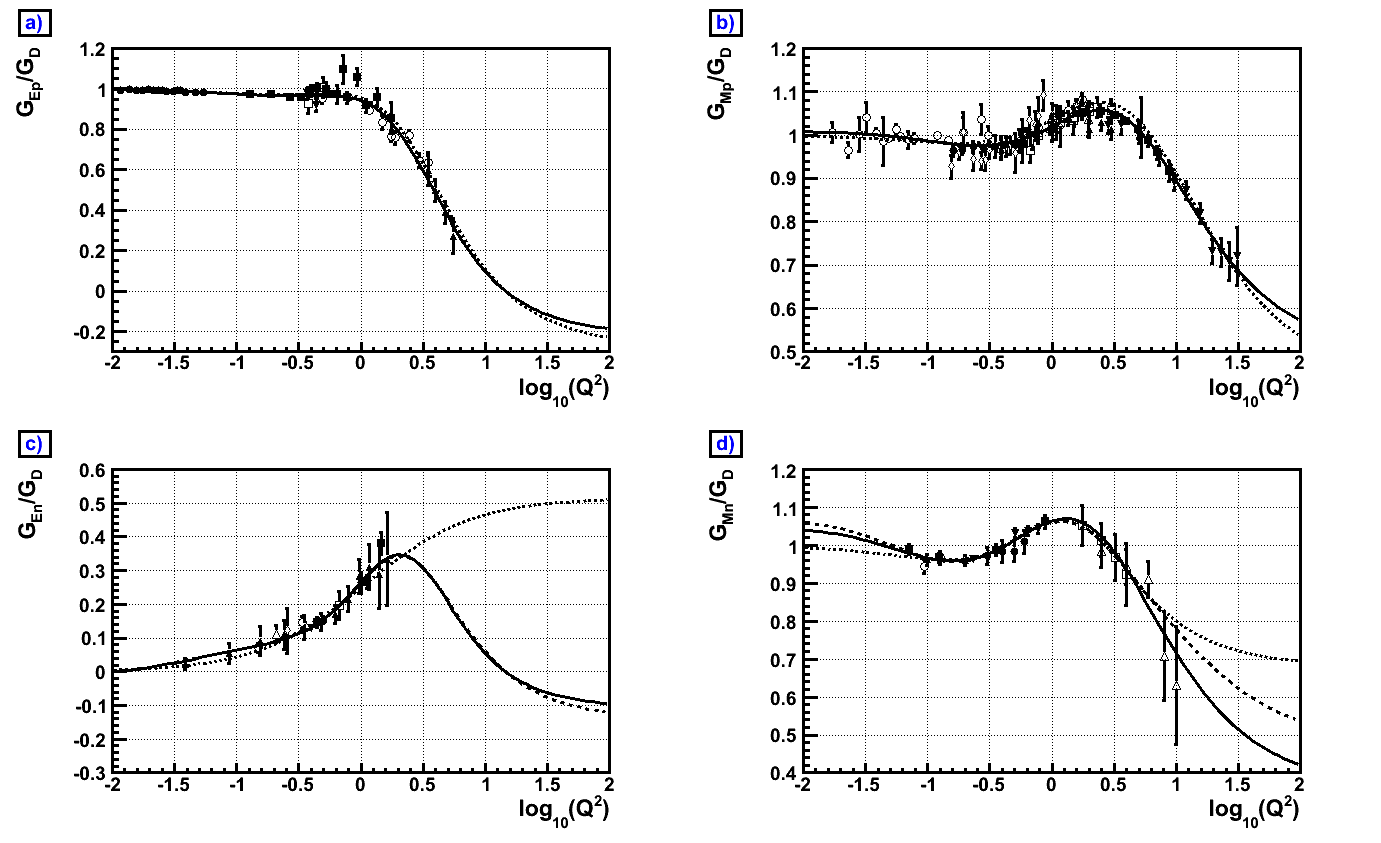
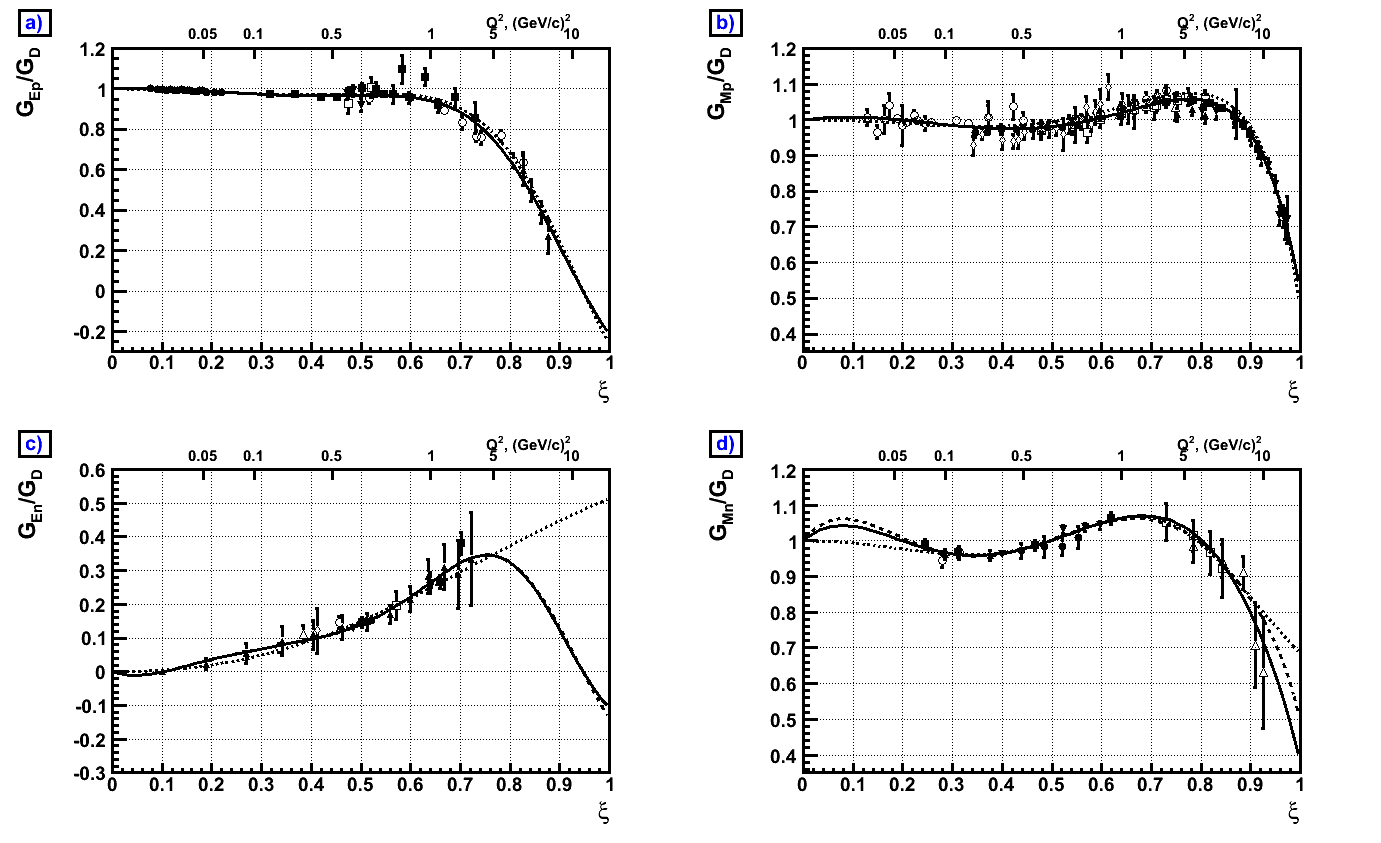
For the Experts, Figure 1 shows are the new form factor fits versus the
square of the momentum transfer (Q2),
and Figure 2 shows the new form
factor fits versus the Nachtman scaling variable x.
Figure 1(a) and 2 (a) show the ratio of the proton electric
form factor to
the dipole form. The solid line is our new duality based fits and the
dotted line is the previous parametrization of Kelly.
Figure 1 (b) and 2 (b) show the ratio of the proton
magnetic form factor to
the
dipole form The solid line is our new duality based fits and the
dotted
line is the previous parametrization of Kelly.
Figure 1 (c) and 2 (c) show the ratio of the neutron
electric form factor to
the
dipole form . The solid line is our new duality based fits (with
d/u->0). The dashed line is our new duality based fits (with
d/u->0.2) , and the dotted line is the previous
parametrization of Galster (also used by Kelly).
Figure 1 (d) and 2 (c) show the ratio of the neutron magnetic
form factor to
the
dipole form . The solid line is our new duality based fits (with
d/u->0). The dashed line is our new duality based fits (with
d/u->0.2) , and the dotted line is the previous
parametrization of Kelly.
Figure 1 (a, b, c, d) versus Q2
`
Figure 2 (a, b, c, d) versus
Nachtman scaling variable x (below)