Electricity and magnetism, the subjects of this course, have a profound influence on life. Electricity and magnetism are distinct manifestations of the same phenomena, called electromagnetism. You are familiar with the role of electromagnetism in static electricity, magnetism, electric power, as well as the myriad applications of electromagnetism to electronics, computers, radio, televison, automobiles. Electromagnetic waves, another aspect of electromagnetism, is manifest by light, radio waves, X-ray, gamma rays, etc. Electromagnetism plays a key role in life; it is electromagnetic radiation that transmits, from the sun, the energy needed to support life on earth. It is the electrical force that binds together atoms, molecules and matter. Nerve cells, the senses of smell, touch, vision all ultimately are electromagnetic in nature. The fascination and beauty of this subject is that the behaviour of electricity and magnetism is unified into one topic, called electromagnetism, which can be condensed into four fundamental laws of nature, called the Maxwell Equations.

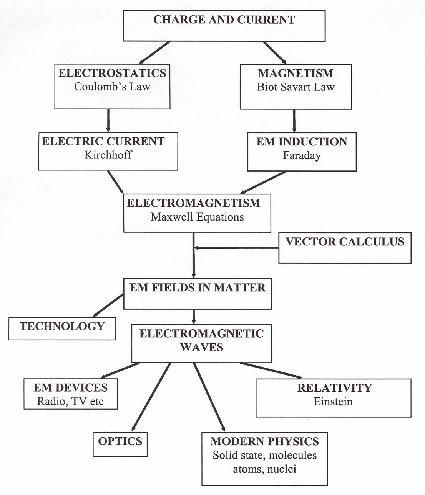
Electromagnetism covers a vast area of science, far more than can be covered during a one term course. However, in one term it is possible to acquire sufficient knowledge of this subject to understand the basic physics underlying many of the above electromagnetic phenomena. It is easy to lose sight of the overall simplicity and unifying aspects of the laws of electromagnetism because of the many new physical concepts to be introduced, as well as the mathematical techniques involved. The first goal of this course is to use experimental evidence to derive in, the simplest form, the Maxwell Equations, which are the basic laws of electromagnetism. The sequence of topics to be studied is illustrated in Fig.1, and is described in the following syllabus.

The existence of charge and current leads first to a discussion of the laws of electrostatics. The laws of electrostatics can be condensed into Coulomb's Law, which exhibits a remarkable similarity to Newton's Law of Gravitation. The concept of the electric field is introduced leading to the flux of a vector field and Gauss's Law. Electric potential, electrostatic forces and energy then are developed. Electric current, due to moving charges, is the following aspect covered. The focus then jumps to the subject of magnetism produced by steady electric currents. Magnetostatics is the magnetic analog of electrostatics and can be described using the Biot-Savart Law. The next important topic is electromagnetic induction. This introduces the dynamic situation where changing magnetic fields produce electric forces, that is Faraday's Law. This provides the key to the interrelation of electricity and magnetism leading to the integral derivation of the Maxwell Equations in vacuo. Maxwell's towering contribution was to add the key ingredient that unified these into the single topic called electromagnetism, and led to the prediction of electromagnetic waves, such as light and radio waves.

The description of the electric and magnetic vector fields is best done using the concepts of flux and circulation of vector fields. These concepts also can be applied to the vector field describing the velocity in fluid flow. Thus the total flux flowing out of a closed surface is related to the loss of fluid from the volume enclosed by the closed surface. The circulation describes the rotation or angular momentum of the fluid flow. The concepts of flux and circulation for fluid flow are very useful when used in conjunction with conservation of both mass and angular momentum for the fluid. Similarly, expression of the laws of electromagnetism in terms of the flux and circulation in the integral form is the simplest for an initial understanding of the subject. However, the expression of the Maxwell equations in terms of the sophisticated vector differential calculus, is far more useful for practical applications of the Maxwell equations. The basic elements of vector differential calculus will be presented following derivation of the integral form of the Maxwell equations in vacuo. The Maxwell equations then will be rewritten in the powerful differential form. The Maxwell equations, in both integral and differential forms, as well as giving a description of the physical consequences, are listed below. The second part of this course will use Maxwell equations, expressed in the differential form, to review the material covered in the first part of the course as well as discuss the consequences of electromagnetism in matter. The course will climax with a discussion of the epitome of Maxwell's contributions, the derivation and description of electromagnetic waves both in vacuum and in matter.

Electromagnetism, as epitomized by Maxwell's equations, led to Einstein's Theory of Relativity. Historically, Einstein's Theory of Relativity was an outgrowth of electromagnetism. Einstein's monumental 1905 paper, that introduced the Theory of Relativity, was entitled ''On the electrodynamics of moving bodies''. Einstein recognized that the Theory of Relativity was a consequence of the Maxwell Equations. He also showed that the magnetic force is related to the electric force between moving charges. Thus the Maxwell equations provide a remarkable unity of fundamental physics. The unity of electricity and magnetism included within the theory of Special Relativity will be the topic of the final lecture.

Electromagnetism is the underpinning of much of science and modern society. From a historical perspective, Maxwell's pivotal contributions will stand out as one of the most important developments of the nineteenth century.

Maxwell's Laws of Electromagnetism

1) Gauss's law of Electricity:

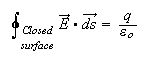
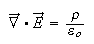
The flux of an electric field through any closed surface is proportional to the enclosed charge.

Conseqence: Like charges repel and unlike charges attract as the inverse square of their separation.


2) Gauss's law of Magnetism:

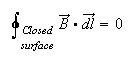
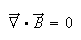
Magnetic flux through a closed surface is zero.

Consequence: Isolated magnetic poles are not observed.

3) Ampére-Maxwell Law:

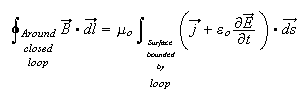
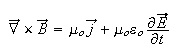
The circulation of the magnetic field around a closed loop is proportional to the rate of change of electric flux through the surface bounded by the closed loop and the electric current flowing through this surface.

Consequence: An electric current or changing electric field induces a magnetic field.

4) Faraday's law of Induction

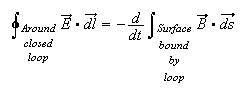
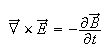
The circulation of E around a closed loop is proportional to the rate of change of magnetic flux through the surface bounded by the closed loop.

Consequence: A changing magnetic field induces an electric current in a loop.


NB) Charge conservation

Charge conservation is built into the Maxwell equations. Often it is convenient to express this law explicitly, namely the flux of a current through a closed surface equals the rate of change of total enclosed charge.
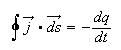
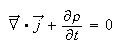