

If this were a real, in-class examination, you would be reminded here of the exam rules, which are as follows. "You may consult only one page of formulas and constants, and a calculator, while taking this test. You may not consult any books, nor each other. All of your work must be written on the attached pages, using the reverse sides if necessary. The final answers, and any formulas you use or derive, must be indicated clearly. Exams are due three hours after we begin, and will be returned to you tomorrow."
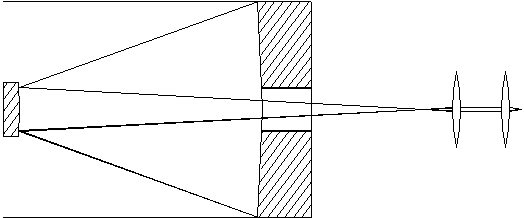
1 (50 points) A 20 cm diameter, 100 cm focal length lens is followed by two smaller lenses, with focal lengths 4.76 cm and 5 cm, as sketched in Figure 1. The first of these lies 104.76 cm past the large lens, and the other lies 9.76 cm further on. All of the lenses are made of flint glass (n = 1.5). The arrangement is used as a telescope, with the large lens as the objective (primary) and with a detector in the final focal plane.
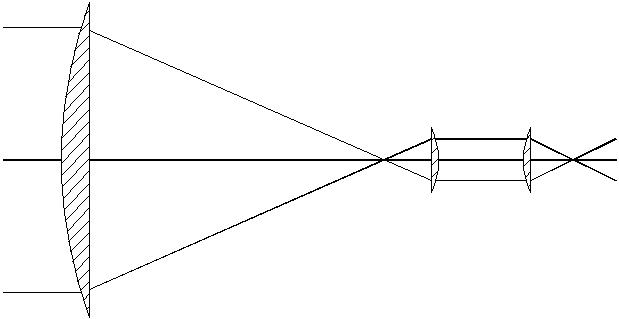
a. Calculate the plate scale in the focal plane. [See solution]
b. Calculate the position and diameter of the pupil that would serve best as a Lyot stop; indicate this position on Figure 1. [See solution]
c. As drawn, the system suffers from a modest amount of Petzval field curvature. Design a field-flattening lens for use at the focal plane that would eliminate this curvature; calculate an index and focal length for this optical element. [See solution]
d. The second lens is replaced by a lens with focal length -4.76 cm, once again made from glass with refractive index 1.5, and the two smaller lenses, still separated by 9.76 cm, are moved closer to the objective, so that the new negative lens is 95.24 cm from the large lens, as shown in Figure 2. The new system has the same plate scale as the old one, and can in principle perform exactly the same tasks.
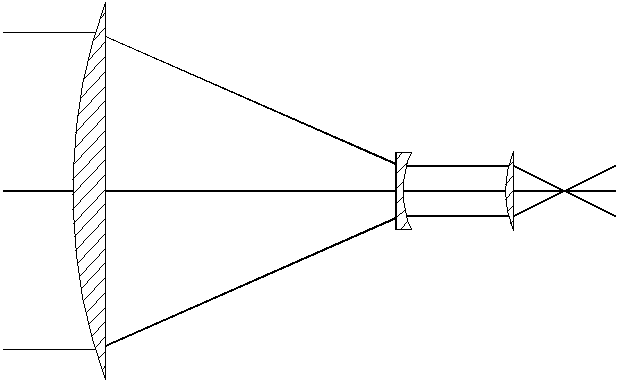
Compared to the previous arrangement, this one has one potential disadvantage and one minor advantage. What are they? (Hint: see parts b and c above) [See solution]
2. (30 points) Coma and astigmatism.
a. Consider observations of a 10 arcminute diameter field at the prime focus of a 6 meter focal length paraboloidal telescope. For what telescope diameter will the effects of coma and astigmatism be equal? Which of these is the larger effect for diameters larger and smaller than this? [See solution]
b. Now consider observations at the prime focus of a 2 meter diameter, 6 meter focal length paraboloidal telescope. For what angular diameter will the effects of coma and astigmatism be equal? Which of these is the larger effect for angular diameter larger and smaller than this? [See solution]
3. (30 points) The spot diagram in Figure 3 was produced in the paraxial focal plane of a spherical mirror 20 cm in diameter. The incident rays were arranged in concentric circles, and spread all the way to the edge of the mirror (like RayTrace's "Bullseye" pattern).
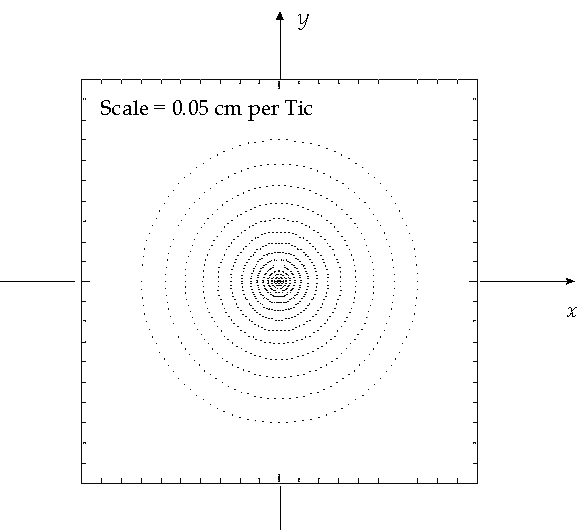
a. On Figure 3, identify the spots corresponding to the rays which reflected from the mirror at coordinates (x, y) = (0, 10 cm), (0, 0), and (0, -10 cm). [See solution]
b. What is this mirror's radius of curvature? [See solution]
4. (50 points) A Gregorian telescope, depicted in Figure 4, has a primary mirror with diameter 2 m and apex radius of curvature 6 m. Its secondary mirror has eccentricity 0.5 and apex radius of curvature 3 m.
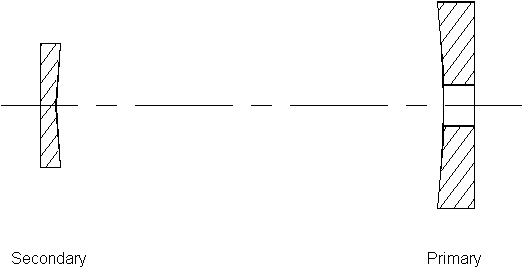
a. Calculate the distances from the secondary mirror's apex to the primary's apex, and from the secondary's apex to the focal plane. [See solution]
b. Calculate the plate scale in the final, Gregorian, focal plane, in arcsec mm-1. [See solution]
c. Consider the primary's edge to be the aperture stop, and calculate the diameter of the telescope's exit pupil, and the distance from this pupil to the secondary's apex. [See solution]
d. Indicate the position and size of the exit pupil on the telescope diagram shown in Figure 4. [See solution]
5. (30 points) A small, concave paraboloidal mirror, with diameter 2 cm and apex radius of curvature 200 cm, is used to make an image of two stars which are separated by an angle of 0.01 radian in the sky.
a. First, the mirror is aligned so that the light from the two stars is incident on the mirror at equal and opposite angles from the paraboloid's axis. Compute the distance between the stellar images in the focal plane. [See solution]
b. Next, the mirror is tilted so that one star's light is incident at an angle 0.1 radian from the paraboloid's axis, and the other star's light at 0.11 radian from this axis. The stellar images in the focal plane remain sharp, but appear to lie further apart than was the case in part a. Which aberration gives rise to this increase in the separation of the images? By how much did the distance between the images increase? [See solution]
6. (50 points) Reflection losses and detector quantum efficiency.
a. Calculate the transmission of the planar surface of a dielectric medium with index of refraction n for light of wavelength l incident normally from vacuum. [See solution]
b. Repeat the calculation for the same surface coated with a plane-parallel dielectric film with index
and thickness
. [See solution]
7. (70 points) Extragalactic observations of the [O III] 0.5007 mm line. A certain spiral galaxy, at rest with respect to the Sun and seen nearly edge-on, emits the [O III] 0.5007 mm line throughout its disk. The galaxy rotates with circular speed 360 km s-1, so that on one side of the galactic nucleus the line appears at l = 0.5013 mm, and on the other side it appears at l = 0.5001 mm.
a. Consider observations of this galaxy with a normal-incidence grating spectrometer, in first order. The groove spacing of the grating is a = 2.0 mm. At what angles (in degrees) will the wavelengths corresponding to the limits of galactic rotation be dispersed? [See solution]
b. At what angle (in degrees) should the grating be blazed, to ensure optimum efficiency? [See solution]
c. A camera lens is used to focus the dispersed light onto a CCD detector array with pixels spaced by 10 mm. It is desired that the wavelength range of galactic rotation correspond to 20 detector spacings. What should the focal length of the camera lens be? [See solution]
d. It is also desired that the wavelength range of galactic rotation correspond to 10 spectral resolution elements (FWHM). How many grating rulings need to be illuminated, and what is the diameter of the beam incident on the grating? [See solution]
e. At l = 0.5007 mm, good Fabry-Perot interferometers have finesse typically equal to 30. In what order would such a Fabry-Perot need to be operated if it were to have the same FWHM spectral resolution as the grating spectrometer discussed above? [See solution]
f. By how much would the Fabry-Perot mirror spacing need to be changed for this order to be scanned over the wavelength range of galactic rotation? [See solution]
8. (70 points) Photon noise and Johnson noise.
a. Starting with the Bose-Einstein probability distribution for photons, show that the standard deviation in photon number per mode in blackbody radiation is given by
![]() ,
,
where, as usual,
![]() .
.
Hint: recall that
![]() .
.
b. A photodetector with resistance R absorbs a single mode and polarization of radiation emitted from a blackbody. The detector is hooked up in a circuit in such a way that there is no DC photocurrent or shot noise present, but only AC currents like those from the photon-number fluctuations calculated in part a. Take the electrical noise power per unit bandwidth dissipated in the detector to be equal to the power fluctuations corresponding to these photon-noise fluctuations, and derive an expression for the standard deviation of current in the detector. Show that in the Rayleigh-Jeans limit (hn ? kT) this expression reduces to the familiar expression for Johnson noise,
![]() .
.
9. (70 points) A Cassegrain telescope, shown in Figure 5, is followed by a pair of lenses set up as collimator and camera. Its parameters are: primary diameter 1 m, primary focal length 2 m, secondary diameter 0.25 m, secondary focal lengths 0.5 m, 2.5 m, collimator focal length 0.2 m, camera focal length 0.1 m, collimator-camera lens separation 30 cm. It is used for observations at a wavelength of 100 mm.
a. What is the FWHM diameter of the diffraction spot at the Cassegrain focus? [See solution]
b. A detector lies at the focus of the camera lens, and is exactly the size of the FWHM diffraction spot at this focus. What is its diameter? [See solution]
c. There is a place between the collimator and camera lenses at which the diffraction-limited beam diameter reaches a minimum. Where is it, and what is the FWHM diameter of the beam there? Sketch of the envelope of the beam as it propagates from the Cassegrain focus, through the two lenses, and arrives at the detector. [See solution]
d. A cryogenic filter with Dl/l = 10-2 and transmission 0.2 is placed in front of the detector, which is also held at a cryogenic temperature. The telescope's temperature is 300 K, and its effective emissivity is 0.1. The detector's quantum efficiency is 0.5, and its photoconductive gain and gain dispersion are both 1. What is the background-limited noise equivalent power (NEP) of the system? [See solution]
e. A certain compact celestial object produces a flux of 1.3´ 10-15 W m-2 at the Earth's surface, within the bandwidth of the filter used in part d. How long would it take the system to detect this object with a signal-to-noise ratio of 10? [See solution]
10. (50 points) Calculate the intensity on a screen in the far field, as a function of angle with respect to the optical axis, of light diffracted by a square aperture with side a.