1) [20 points]

Consider an object of mass M moving in the gravitational field near the surface of the Earth. Assume the object is moving in the up-down direction only.

a) [4 pts] Show, using the definition of acceleration and Newton's 2nd Law, that the velocity of the object at any time t is given by

where v>0 means the object is going up, v<0 means the object is going down, and v(0) is the object's initial velocity at time t=0. g is the gravitational acceleration constant g = 9.8 m/s².

Hint: use the definition of acceleration.

b) [4 pts] Use the law of conservation of energy to show that the object's height at time t, is given by

where h(0) is the object's initial height at time t=0, and  is the square of the velocity at time t.

c) [4 pts] Combine the results of parts (a) and (b) to show that the object's height as a function of time, is given by

Hint: substitute the equation in part (a) into the equation in part (b).

d) [4 pts] Suppose a cannon ball of mass 1 kg is shot straight upwards with an initial velocity of 200 m/s, from an initial height of h(0)=0. What is the maximum height that the cannon ball reaches?

Hint: at it's point of maximum height, the cannon ball's velocity is v=0.

e) [4 pts] If the cannon ball of part (d) if fired at time t=0, at what time does it hit the ground?

Hint: when the ball hits the ground, its height is at h=0.

________________________________________________________________________

2) [10 points total]

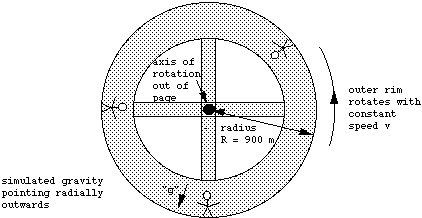
Deep out in space, a space station in the shape of a wheel, is set spinning with constant rate of rotation about its axis, as in the picture below.

a) Explain how this serves to simulate a gravitational force pointing radially outwards towards the rim of the wheel. In other words, if an astronaut in the space station were to let go of a ball, he would see it "fall" towards the outer rim of the wheel. Explain why.    [5 pts]

Hint for both parts: If the astronaut is standing still (with respect to the rotating space station) on the outer rim as shown in the diagram, he is in fact moving in uniform circular motion, as seen by someone outside the space station. If he is so moving, he must be experiencing a centripetal acceleration. What force on the astronaut is causing this centripetal acceleration? If the astronaut holds a ball, the ball too has the same centripetal acceleration. What is the force on the ball causing this acceleration? Does this force act once the astronaut lets go of the ball? How does the ball move when the astronaut lets go?

b) If the radius of the space station is 900 meters, what should be the speed v of the outer rim of the wheel so that this simulated gravity at the outer rim of the wheel is exactly equal to that felt on the surface of the Earth? What will be the corresponding period of rotation of the space station? [5 pts]