We now leave probability for the moment, and start our discussion of the basics laws of physics: Newton's Laws of Motion.

1) An object at rest stays at rest, and an object in a state of motion in a straight line with constant speed stays so moving, unless the object is acted upon by external forces. (Law of Inertia)

2) When an external force acts on an object, the acceleration, which is the rate of change of velocity with time, is proportional to the external force. The constant of proportionality is called the inertial mass of the object. In mathematical notation,  (the arrows over the symbols indicate that they are vectors - we will explain what a vector is shortly).

3) Forces come in equal and opposite pairs -"for every action there is an equal and opposite reaction". If particle A exerts a force on particle B, then particle B exerts a force equal in magnitude but opposite in direction, on particle A.

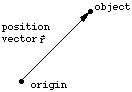
In order to use Newton's Laws of motion to describe how objects move when acted on by forces, we need first a mathematical concept to describe the position of objects, and their motion. This is the vector. A vector is something that specifies both a magnitude and a direction. The simplest example of a vector is the position vector.

The position vector locates the position of an object with respect to some fixed point in space, which we call the "origin". We can graphically represent the position vector as an arrow pointing from the origin to the location of the object. The magnitude of the position vector is just the length of the arrow, or equivalently the distance between the origin and the object. We denote the position vector by the symbol  (with an arrow above), and the magnitude of the position vector by the symbol  (without the arrow above).

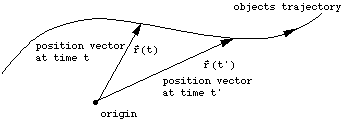
For an object which is moving along a trajectory in space, we can describe the position vector of the object as it varies in time by the symbol , which is read as " as a function of t", and means that the object is at position  at time t.

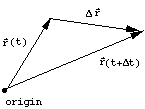
Addition of vectors

Suppose one is at position  at time t, and at position  a small time  later (in physics notation,  usually means a small increment in something; here is a small increment in time). If we draw the arrow starting from the tip of  and ending at the tip of , we call this the difference vector .

If we think of the position vector as the straight line path we must walk along to arrive at the point  when starting from the origin, then  gives the straight line path we must walk along to arrive at the point  when starting from the point . We can thus write

and interpret this addition of vectors geometrically as follows: to go from the origin to the point  we can either go in a straight line directly to , or else we can go first to the point  and then walk along the straight line path given by . Both these two routes wind up at the same end point .

We can add many vectors up the same way. Just place the arrows end to end, one after the other to get:

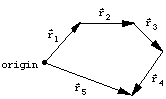
Walking along the path specified by the vectors , , , and  is equivalent to taking the straight path along .

Using this definition of addition of vectors, we can also define the difference between two vectors:

Note that when we write the vector equation  it does not mean that the total distance traveled in walking along the path described by  is the same as the total distance traveled in walking along the straight path described by the vector . This is obvious from the figure above. In terms of the magnitudes of these vectors, . It is only in terms of the full vector quantities, which include the direction, that the vector equation gives an equality.

Circular Motion - velocity and acceleration vectors

Consider an object traveling clockwise in a circular orbit of radius r, going around the circle with a constant rate of rotation (such as does a hand of a clock). The distance the object travels in going one complete turn around the orbit is the circumference . The time it takes to do so is called the period of the orbit, and we denote it by the symbol . The average speed v of the object is then

speed = distance/time, 

We now define the velocity vector. Consider how the position vector changes as the particle moves from time t to time . We take as the origin the center of the circle.

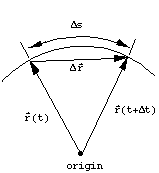
The average velocity  between times t and  is defined as the time rate of change of the position vector:

The instantaneous velocity vector at time t is then given by the above, as we take the time difference .

To compute , note that as  the displacement vector  gets smaller and becomes equal in magnitude to the arc length . Since the object is going around the circle at a constant rate, the ratio of the length  to the entire circumference  is equal to the ratio of  to the period of the orbit . So

The magnitude of the velocity vector is then

Thus the magnitude of the instantaneous velocity vector, called the instantaneous speed, is just equal to the average speed around the circle. This is reasonable since we said that the object is going around the circle at a constant rate.

The direction of the instantaneous velocity vector is obtained by looking at the above diagram as  the two radial position vectors get closer and closer, and the direction of  becomes tangent to the circle. Since the direction of  is determined by the direction of , we conclude that the velocity vector   always points tangent to the circle, perpendicular to the position vector  . (Henceforth we will always mean the instantaneous velocity whenever we say simply "velocity", unless we explicitly indicate otherwise.)

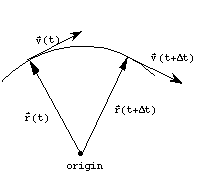
In general, the velocity is a vector whose magnitude is equal to the instantaneous speed, and whose direction points tangent to the direction of motion.

We now define the acceleration vector . The acceleration vector is the time rate of change of the velocity vector:

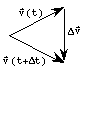
where one is to take the limit as . We define geometrically the velocity difference vector  as shown above, in analogy to how we defined the position difference vector. To compute the magnitude of  as , we use an argument similar to the one we used to compute the magnitude of . Since  has a constant magnitude independent of time, we can draw the vectors  as radii of a circle of constant radius v.

As , the length of  become equal to the arc length of the circle between the points  and . Now since  is always perpendicular to , the angle swept out on the above circle as  rotates into , is the same as the angle swept out as  rotates into . Since the rate of rotation is constant, this angle is in the same ratio to the total angle  as the time difference  is to the total period of the orbit . Therefore the arc length  is in the same ratio to the total circumference of the above circle , as  is to . We thus have

so the magnitude of the acceleration vector is

Using our earlier result that , we can rewrite the above by either substituting for v in terms of r and , or by substituting for  in terms of v and r, . We then get the equivalent expressions

The direction of the acceleration vector is obtained by noticing that as , the direction of  becomes perpendicular to the vector . Now since we already found that  is perpendicular to the position vector , we conclude that the direction of , and hence the direction of  points opposite to the direction of , that is  points inwards to the center of the circle.

We therefore see that an object going around in a circle at constant speed, is experiencing an acceleration which is constant in magnitude, but whose direction is constantly changing so that it always points to the center of the orbit. This is known as the centripetal acceleration of an orbiting object. Since the object is experiencing an acceleration, Newton's second law, , tells us that the object can only move in such an orbit if there is a force acting on the object that is constant in magnitude and pointing towards the center of the orbit (since acceleration is a vector, so must be force). For a planet orbiting the sun, this force is the gravitational force from the sun. For a ball being swung around on the end of a string, this force is the line tension of the string. If at any point the force is turned off (for example the string is cut), the ball will cease its circular motion and fly off in a straight line path tangent to the circle.

Note: it is a common misconception among begining physics students that if an object is moving along a certain trajectory, then there must be a force which is pushing that object along on this trajectory, and that the force is therefore pointing in the same direction as that in which the object is moving. Our example of an object in circular motion shows this notion to be in general false: in the case of circular motion, the acceleration  points perpendicular to the objects direction of motion!

To summarize: an object moving around in a circle of radius r, at a constant rate of rotation with the period of orbit , has:

velocity vector   whose magnitude is the constant speed

and whose direction is always tangent to the circle in the direction of motion; and

acceleration vector  whose magnitude is the constant

(where the second equality comes from substituting in for v from above)

and whose direction is always pointing to the center of the circle.

A Word About Units of Measure

Since we are discussing position, time, mass, velocity, acceleration, and force, it is necessary to use a system of units in which we can record measurements. The universally used system in physics is the metric system in which

length is measured in meters, abbreviated by m

time is measured in seconds, abbreviated by s

mass is measured in kilograms, abbreviated by kg

with these basic units,

velocity = length/time is measured in m/s

acceleration = velocity/time is measured in m/s²

force = (mass)(acceleration) is measured in kg m/s² = nt

The unit of force, kg m/s², is given the special name, the "newton", and is abbreviated by the letters "nt" or sometimes by "N".

The above is also referred to as the "MKS" system of measurement.