Galileo (who came before Newton) is credited with the observation that objects dropped from a fixed height, fall to the ground with a motion described by a constant acceleration downwards. From this observation and his second law, , Newton concluded that the gravitational force near the surface of the earth has a constant magnitude, and points down towards the center of the earth (if  is constant, then  will also be constant).

Galileo also observed that objects of different weight, when dropped from the same height, will hit the ground at the same time. (This observation has of course its limitations - if you drop a ball and a feather from the same height, of course the ball hits the ground first. This has to do with the frictional force of the air acting on falling objects, known as the "air resistance". However, if you dropped the ball and the feather inside a tube from which all the air had been pumped out, you would see that the ball and the feather do indeed hit the bottom of the tube at the same time!) From this, Newton concluded that the gravitational force acting on an object must be proportional to the mass of the object, , since then Newton's second law would give:

Canceling the common factor of m on both sides gives:

Thus the acceleration of the falling object is constant and independent of the object's mass. Since acceleration is the time rate of change of velocity, and velocity is the time rate of change of position, objects dropped from the same height will feel the same acceleration, and so move with the same rate of increasing velocity, and so hit the ground at the same time, independent of their masses. The direction of  points downwards towards the center of the earth, and the magnitude of  is measured experimentally to be .

Note that this need not have been so. There is no a priori reason why the gravitational force had to be proportional to the mass of a falling object. For example the electric force on an object is proportional to the object's charge, and objects of equal charge may have different mass. When we wish to distinguish between the mass "m" that enters the law of gravitation, , and the mass "m" that enters Newton's second law,  (where here  can be any force at all, not just the gravitational force), we refer to the first as the "gravitational mass", and the latter as the "inertial mass". That the gravitational mass is always exactly equal to the inertial mass (and so we refer to them both as simply the "mass") is a profound experimental fact about nature. There is no reason it had to be this way, nature is just found to be like this!

This equality of gravitational and inertial mass has some interesting consequences. Consider, for example, traveling in an elevator. If you hold out a ball and let go, you will see it will fall to the bottom of the elevator. This is because the floor of the elevator is supporting you, counter-balancing the force of gravity acting on you, while once you let go of the ball, there is nothing counter-balancing the force of gravity on the ball so it accelerates downward. Now imagine that the elevator cable suddenly breaks, and so the elevator and everything in it is now in a state of free fall. Due to the equality of gravitational and inertial mass, everything in the elevator is falling to the ground with the same constant acceleration g. The floor of the elevator is no longer supporting you against the force of gravity. Now if you let go of a ball, you will see it just hanging there in front of you! This is because both you and the ball are accelerating downwards with the same acceleration g. Both you and the ball will hit the ground at the same time. Since you and the ball are both moving downwards in exactly the same way, the ball will not fall any faster than you do, and so from your vantage point the ball will appear just to hang there in front of you. For an observer in free fall with the elevator car and all its contents, the force of gravity appears to have disappeared! - objects when dropped, no longer fall to the bottom of the elevator car! This is in practice how astronauts train for the weightlessness of space. They go up in a big plane, which then takes a nose dive downwards. Everything inside the plane is then is a state of free fall and so simulates the weightlessness of space.

The observation that, as a result of the equivalence of gravitational and inertial mass, one can make the effects of gravitation seem to disappear by going to an accelerating "frame of reference" (in the above discussion this is the freely falling elevator car, or the nose diving airplane) formed the basis of Einstein's General Theory of Relativity.

Returning to gravity, Newton was trying to explain the motion of the moon in orbit around the earth. From his laws of motion Newton realized that the moon, going in its uniform circular motion around the earth, must be experiencing a centripetal acceleration directed towards the center of the moon's orbit, i.e. towards the earth. He therefore concluded that there must be a force acting on the moon which is also directed towards the earth. He then made the very bold assumption that the force that attracts the moon to the earth is the same force that makes an apple fall to the surface of the earth, i.e. gravity. Newton's idea that it is the very same force of gravity that determines both the motion of ordinary objects at the surface of the earth, and the motion of the moon and the planets, was quite revolutionary by ancient standards; to ancient minds planetary, or heavenly, motions were attributed to celestial or god-like processes very far removed from the mundane behavior of ordinary objects. Newton's theory of gravitation was therefore the first examples of a universal theory of nature - Newton's laws of mechanics, and his theory of gravity, applied not only on earth to ordinary objects, but everywhere in the universe to all kinds of objects.

Newton next needed to figure out the exact mathematical form of the graviational force that acts between the moon and the earth, and similarly between the sun and the planets. To do so, he made use of the observational results compiled by the astronomer Johanes Kepler.

Kepler found, by analyzing the motion of the planets, that if  was the period of orbit of a given planet, and r was its distance from the sun, then the ratio  was a universal constant, having the same value for all the planets.

Newton found that he could explain Kepler's observation by assuming that the magnitude of the force attracting a planet to the sun was proportional to the mass of the planet, and inversely proportional to the square of the distance of the planet from the sun, i.e. if it had the mathematical form,

where C must have the same numerical value for all the planets. To see how this gives rise to Kepler's law, remember that the centripetal acceleration of the planet in its uniform circular motion has magnitude

Applying Newton's 2nd law,, using the gravitational force and centripetal acceleration given above, then gives

Multiply both sides by , and divide both sides by  to get

If the constant C has the same numerical value for all the planets, this then explains Kepler's observation!  for each planet must have the same constant value . (Note that in the above we have written the equations in terms of the magnitudes of the vectors, and not in terms of the vectors themselves. We can only do this because in this case the force vector and the acceleration vector are pointing in the exact same direction, from the planet to the sun.)

Newton observed that the force of the sun on the planets, and the force between a falling object and the earth, were both proportional to the mass of the object experiencing the force. This strengthened his idea that both effects are due to the same force of gravity. Newton now made a very bold and not at all obvious assumption - Newton assumed that all objects of matter in the universe, no matter how big or small, no matter whether on earth or out in space, attract each other with the same gravitational force. From Keppler's astronomical data, this force should be proportional to the inverse square of the distance between the centers of the objects. From Galileo's and Keppler's observations, the gravitational force acting on an object should be proportional to the mass of the object. And now from Newton's third law of action and reaction, if object #1 exerts a gravitational force on object #2 (and so this force is therefore proportional to m₂, the mass of object #2) we must also have that object #2 is exerting an equal and opposite force on object #1. Since this reaction force is a gravitational force acting on object #1, it must therefore be proportional to m₁, the mass of object #1. Putting it all together, Newton concluded that the general form for the magnitude of the gravitational force acting between objects of mass had to be

where  and  are the masses of the two objects,  is the distance between the two objects, and G is a fundamental constant of nature which has the same value everywhere in the universe (going back to our discussion above, the constant C in Keppler's data is now just ). The numerical value of G in MKS units is . The gravitational force is always attractive, so the direction of the force acting on mass  points towards mass , and the direction of the force on  points towards .

One can measure the gravitational constant in the laboratory with a device known as the Cavendish balance - this consists of a "dumbbell" of small lead balls suspended by a wire, with a dumbbell of much larger lead balls mounted on a rotating frame about the small dumbbell. When the large dumbbell is rotated (care is taken to isolate all mechanical vibrations due to the moving large dumbbell from influencing the suspended small dumbbell), the changing gravitation forces that the large dumbbell exerts on the small dumbbell causes the small dumbbell to rotate as well. Measuring the angular deflection of the small dumbbell, and knowing the masses of the balls and the distance between them, allows one to determine G. The force of gravitation truly acts not just between astronomical bodies but between all objects with mass.

The above force law has one technical problem. What happens if the objects involved are very large, so that the mass of the object is distributed over some volume of space, and is not all located at one point. If so, then what distance should be taken as  in the above? Should it be the distances between the surfaces of the objects? or between the centers of the objects? or something else? This question is potentially of concern in computing the forces between the planets and the sun (although in this case, the distances of separation are so much larger than the radii of either the planets or the sun that it seems reasonable to regard each as approximately a point mass); it is certainly of concern in computing the force between a falling apple and the earth - the apple is attracted by all the mass of the earth which is certainly spread out over a distance which is huge compared to the size of the apple or the distance of the apple above the ground.

In principle the answer is that one must divide the large object up into many infinitesimally small pieces of mass, and apply the force law to each tiny piece using the distance between that piece and the second object that the large object is attracting. The total force is just the sum of all these many pieces. However Newton figured out (the proof is too complicated for us here) that, provided the mass of the large object is distributed in a spherically symmetric way about the center of the object, the forces from all the different pieces of the object combine to give a total force that looks just like all the mass of the object was concentrated exactly at the center of the object. Since the sun, the earth, and the planets are very closely spherical, the gravitational forces between them should thus be calculated taking distances measured from the center of these bodies.

We can now relate the gravitational constant G, to the gravitational acceleration at the surface of the earth, g. In computing the gravitational attraction between the earth and a falling apple, we should take all the mass of the earth, call it , and view it as concentrated at the center of the earth. If the apple is at height h above the surface of the earth, the distance between the apple and the center of the earth is , where  is the radius of the earth. The force pulling the apple of mass  downwards therefore has magnitude

But the height h is so much smaller than the radius of the earth , that we may, to a very high degree of accuracy, ignore its contribution in the denominator above. We then get

Comparing the above to , the form for the gravitational force at the surface of the earth, and canceling out the common factor of , we get

Thus, by measuring the gravitational constant G and the gravitational acceleration g in the laboratory, we get a relationship between the mass of the earth and its radius! If we know that the radius of the earth is  (a fact known to the ancient Greeks), then knowing the values of G and g allow us to calculate the mass of the earth as .

Example - the weightlessness of space

You are all familiar with the phenomenon that astronauts orbiting the earth in a spaceship experience weightlessness - gravity seems to disappear. What is the origin of this effect? Has the spaceship gone so far out from the earth that the earth's gravitational force on the spaceship and its contents has become negligible?

The spaceship has certainly not escaped the gravitational force of the earth! The fact that the spaceship is orbiting the earth with a circular motion means that it is always accelerating towards the center of the earth, and so must be experiencing a force pulling it to the center of the earth - this is just the gravitational force of attraction to the earth. If the spaceship was not feeling the gravitational force of the earth, it would shoot off into space instead of orbiting around the earth!

In particular we saw that the magnitude of acceleration of this circular motion was  or equivalently , where  is the speed of motion around the orbit. If the spaceship has mass m, then this acceleration must, via Newton's second law, be balance by the gravitational force from the earth. Using Newton's law for the gravitational force in Newton's 2nd law of motion,, we get

where we have canceled the common factor m, and multiplied both sides by r. Thus the velocity of the orbit does not depend at all on the mass of the spaceship. Similarly, the velocity of any object inside the spaceship behaves the same way - it is independent of the mass of the object. So all objects inside the spaceship are orbiting with exactly the same speed, and experience exactly the same acceleration. The force of gravity causes each and every object inside the spaceship to orbit in exactly the same way and so, as in the case of the falling elevator car, to someone inside the spaceship it looks as if gravity has disappeared! The orbiting spaceship is another example of a "frame of reference" which is experiencing "free fall".

Note that the above is, as in the case of the falling elevator car, a direct consequence of the equivalence of gravitational and inertial mass.

Universality of the Law of Gravitation

To illustrate more clearly the fact that Newton's Law of Gravitation is a universal law of nature, that works equally well between objects on earth as it does between astronomical bodies, consider the two situations of the moon orbiting the earth, and an apple falling to the ground. The force on the moon from the earth, and the force on the apple from the earth are

where, , and  are masses of the earth, moon, and apple respectively,  is the radius of the moon's orbit, and  is the radius of the earth. Now we also know that the force on the moon is, by Newton's second law, equal to the mass  times the centripetal acceleration, and we know that the force on the apple can be expressed in terms of the gravitational acceleration at the surface of the earth, g. We thus have

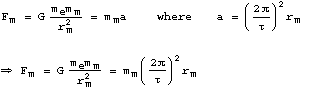
and

where  is the period of orbit of the moon about the earth. Canceling the common factor  from both sides of the equation for , and canceling the common factor  from both ides of the equation for , they give

and 

Multiplying both sides of the first equation by , and both sides of the second equation by , then gives

Since the left hand sides of both the above equations are equal, we can now equate the right hand sides to get

Notice that the left hand side of the above equation involves quantities that pertain only to the earth, while the quantities on the right hand side pertain only to the moon! That there should be any relation at all between the two sides is an astounding, and highly non-trivial, consequence of Newton's theory.

To check the above relation, we can put in the numbers: , , , and . We then get for the left hand side, , while the right hand side is, .

These two values are 0.5% of each other! This is a pretty good confirmation of Newton's theory. Why is the agreement not exact? There are several corrections that must be considered: (1) The force from the earth on the moon also results in an equal and opposite force on the earth from the moon (Newton's third law). Thus the earth is accelerated and is not stationary at the center of the moon's orbit as we have assumed. Since the mass of the earth is much greater than the mass of the moon (and so the acceleration experienced by the earth is much smaller than that experienced by the moon) this is a small but noticeable correction; (2) The mass of the earth is not distributed perfectly spherically - the rotation of the earth causes it to bulge out slightly at the equator. This leads to a correction since we assumed that the gravitational force from the earth could be treated as if all the mass was concentrated at the earth's center - this is only strictly true for a perfect spherical mass distribution; (3) The orbit of the moon is not perfectly circular; (4) The gravitational force of the sun also influences the motion of the moon around the earth. When these and other similar corrections are included, the small difference between the left and right hand sides of the above equation can be satisfactorily explained.