We now want to introduce a crucial concept that runs throughout all of physics. This is the notion of energy, and the corresponding law that states that in all physical processes, the total energy, summed over all its various parts, will always be constant.

To make an analogy, imagine a primitive economy consisting of various material objects, each of which has a unique and well defined "value" associated with it. A person has a certain amount of money, which also has associated with it a well defined "value". The person may now exchange his money for material objects, and then sell these material objects to make back money, and so on. But in each exchange, the total "value" owned by that person remains the same. At any particular time that "value" may be distributed in different forms, consisting of a certain amount of money, and a collection of various material objects. But the total value remains the same (this of course is a very idealized economy - in real life, the value of material objects can certainly change with time).

Energy is like the "value" of the physical world. It can exist in various forms, like "kinetic energy" (analogous to a "material object"), or "potential energy" (analogous to "money" - it represents the potential to acquire material objects). But in any physical process, the total amount of energy summed over all its forms must remain constant. One of the main ways that physics has progressed over the years, is through the discovery of new forms, or representations, of energy.

We now want to make these ideas concrete through the use of a specific example. We will consider the case of an object of mass M, falling in the gravitational field near the surface of the Earth. We will see that its energy is made of two pieces: the kinetic energy which is determined by the speed of the object, and the gravitational potential energy which is determined by the height of the object.

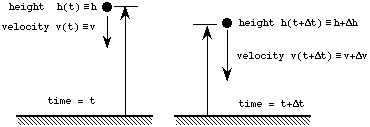
At time t, the object is at height h above the earth. At time  later, it has fallen to height , where  is therefore a negative amount. At time t the object had velocity v, directed downwards. At time  the velocity has increased to an amount . Imagine that the time interval  is very small. First, we note that the change in velocity is due to the acceleration that the object feels, falling in the gravitational field of the Earth. Since the acceleration of a falling object is always the gravitational acceleration ,

we have from the definition of acceleration,

We can also relate the change in height  to the velocity v by

(the minus sign is because we have chosen to measure h as pointing upwards, while we measure v as pointing downwards.)

Combining the last two equations in each line one gets

or

We want now to understand the meaning of the term .  is the change in velocity in time . Consider now how the square of the velocity changes over this same time.

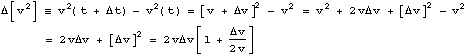
Now our starting assumption was that  was very small. If so, then the velocity cannot change by very much, and so  must be very small compared to v. Hence  and the term in the brackets at the end of the last line of the equation above is to a very good approximation just unity. We therefore have, in the limit that  gets vanishingly small,

      and so      

where the last equality follows since 1/2 is a constant number that does not change with time. Similarly we can write  since g is a constant that does not change with time. So finally we have

So the combination  does not change its value over the interval of time . Similarly we can consider the time interval  to , and again we must find that  does not change its value. Proceeding in this fashion, adding up more and more time intervals  we have the result that

   =   constant over entire time of object's fall.

If we now multiply the above by the object's mass M, this defines the energy E

which is constant over the entire time of the object's fall. The reason we multiply by the mass of the object M, in order to define the energy, is as follows: If we had two such equal objects falling at the same time, it would be natural to suppose that the total energy of the two objects is just twice the energy of one object alone. Now imagine that these two objects are attached, and so can be viewed as one single object of twice the mass as each original object. Clearly the energy is still twice the energy of one of the original objects. This argument suggest that the total energy of an object should be proportional to the amount of mass in the object, hence  as in the definition above.

The two parts of the energy above have special names. The first part, determined by the velocity of the object, is called the "kinetic energy". The second part, determined by the height of the object, is called the "gravitational potential energy" of the object. As the object falls, v increases while h decreases. Kinetic energy is gained while potential energy is lost. But the sum of kinetic plus potential energy always remains constant.

The kinetic energy term should seem reasonable to you: we are used to the idea that an object which is moving with velocity v has an energy that increases as v increases. The second term for potential energy might seem less clear. Consider a ball lying at the top of a cliff at height h, which is not moving at all, ie. v=0. Why should we regard this ball as being any more energetic than a ball which is lying with v=0 at the bottom of the cliff? The reason is because if the ball at the top of the cliff is moved just slightly to the edge of the cliff, it will fall off. In the process of falling, its velocity will increase, and by the time it reaches the bottom, it will be moving with a rather fast velocity, and so indeed be more energetic than the ball which was initially placed at the bottom of the cliff. Unless we want to assume that the ball on the top of the cliff initially had zero energy, but that it somehow acquired energy during its fall (this would mean energy was NOT conserved), we must associate a certain amount of energy with the ball's height above the bottom of the cliff. This is the ball's potential energy. Alternatively, we can regard the potential energy as the energy that one would have to expend in order to carry the ball from the bottom of the cliff and place it at the top of the cliff, in the first place.

We can use conservation of energy as a tool to find out many interesting things about the motion of falling objects. For example, consider the ball of mass M falling off the cliff of height . Initially, the ball is not moving, so v=0, and the ball's energy is made entirely of its potential energy

Later, when the ball has fallen to height h, its energy can be written

where v above is the speed at height h. Since energy is conserved, the energy above must be equal to the inital energy, so we have

Therefore

      and so      

or

The above gives the object's velocity v, as a function of its height h. When the object hits the ground, h=0, and its final velocity will be

Example

Let us consider an example, to illustrate some of the ideas of this section on Newton's equations and energy conservation.

A block of ice, with mass M = 1 kg, slides to the right (with no friction) across a smooth surface with a velocity of v=2 m/s (see diagram below). The block is initially 3m from the start of the incline.

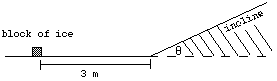
a) How long does it take the block to reach the incline?

b) The block starts up the incline, and comes to rest after traveling for 1/2 s up the incline. What is the acceleration acting on the block while it is on the incline? (the acceleration acting on the block is constant while it is on the incline)

c) What happens after this? (the block has come to rest - now what does it do?)

d) How high above the initial flat surface does the block get, before it stops and slides back down?

e) Given the answer to (b) and using the value of the gravitational acceleration , find the angle of the incline .

Solution:

a) The block moves with a constant velocity v=2 m/s before it reaches the incline. Using , with  the distance to be traveled, we get for the time

b) During the time the block is on the incline, its acceleration is a constant. We know this to be true since Newton's 2nd law says that the block's acceleration is determined by the forces which act on it. These forces are the force of gravity pulling downwards, and the reaction force from the surface of the incline pushing upwards perpendicular to the surface of the incline. Neither of these forces are changing in time, and so the acceleration cannot be changing. The acceleration, in the direction parallel to the surface of the incline, is then given by

where, since a is constant, we can take the interval  to be any finite time interval during which the block is on the incline. Let us take to be the time between the block first arriving at the incline, and the block coming to rest. We are told that . The corresponding  is the velocity difference between the block at rest, v=0, and the block initial velocity when it first reached the incline, v=2 m/s. So    .   Taking the ratio, we find that

the minus sign indicates that the acceleration is in the direction pointing downwards along the surface of the incline.

c) When the block has come to rest, it has converted all of its initial kinetic energy into potential energy. When it is at rest, it still experiences an acceleration a down the slope of the incline, since as explained in (b), the acceleration is always constant when the block is on the incline. The block will thus start to increase in velocity moving backwards down the plane. Since energy is conserved, as the block's height decreases, its kinetic energy increases. The block moves in exactly the reverse way as it did in climbing the incline. When it hits the flat plane again, all its potential energy is converted back into kinetic energy, and so its speed must again be exactly 2m/s, as it was initially. Only now the block is moving in the opposite direction to the left.

d) The easiest way to do this part is to use conservation of energy. We have

where the energy E is constant over the motion of the block. At the point when the block first reaches the incline, h=0, and so the energy is entirely kinetic energy, so

          where v = 2 m/s is the block's initial velocity

When the block reaches its highest point and starts to fall back down, v=0, and so the energy is now entirely potential energy

            where h is the maximum height

Equating the two results for the energy above gives for the maximum height h,

       and so              and so       

Using v = 2 m/s and , we get

e) To do this part, consider the vector of the gravitational force  acting on the block to be written as the sum of two other vectors pointing in directions parallel and perpendicular to the surface of the incline , as shown in the picture below. That  and  do indeed sum up to  is illustrated by the diagram to the right, which gives the definition for the addition of vectors.

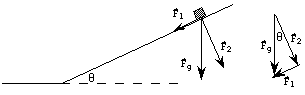
The force , pulling down perpendicularly to the surface of the inclined plane, is exactly balanced out by the reaction force (also called the "normal" force) from the surface of the incline, pushing up against the block - this is the force that keeps the block from falling through the surface of the incline. It is the force  that determines the blocks acceleration a along the surface of the incline.

Using elementary geometry, one can show that the angle between the vectors  and  is just the angle  of the slope of the incline. From trigonometry, we have that the magnitude (length) of  is related to the magnitude of  by

Now since by Newton's 2nd law, , and since the form of the gravitational force near the surface of the earth is,, we have for the magnitude of the acceleration

so

So the angle  is given by