In the remaining section of this course we want to discuss the atomic theory of gases. In particular we will work towards answering the following two questions:

1) We are all familiar from high school chemistry with the atomic theory of matter. All substances are made up of fundamental building blocks of matter, known as atoms. The ratio of the weights of atoms are very close to being simple integers, thus suggesting that the atoms themselves are built out of more fundamental building blocks (neutrons and protons, which are very close to equal in weight). Atoms can bind together to from clusters, known as molecules.

This atomic theory of matter has been around as a modern scientific theory (as opposed to a Greek philosophical idea) for about 200 years. However it is only relatively recently that science has given us new sophisticated forms of microscopes which enable us to directly image the structure of matter at the atomic scale. How then did scientists arrive at the atomic theory of matter before any such microscopes were invented? How did they know that matter was comprised of small individual particles, and not a smooth continuum?

2) In our experiment of ink diffusing into water, we found that the speed of the ink particles, in-between their collisions with the water molecules, was about 10⁵ cm/sec. Why is this speed so large? What parameters of the experiment determine this to be the speed?

The Ideal Gas Law

We will start by answering the first question above. By imagining a series of four different experiments probing the properties of a gas, we will indicate how one arrives at the atomic theory of matter.

Properties of a gas:

1) A gas expands to fill up all available volume. If you let a gas out of a closed box, it will expand to fill up the entire room.

2) A gas exerts pressure on the walls of its enclosing container. You are all familiar with the pressure that the air inside a rubber tire exerts to keep the tire inflated, or the pressure of the air inside a balloon that stretches the balloon out to an enlarged shape. Pressure is just force per unit area: P = F/A. If a gas exerts a pressure P on a wall of area A, the wall experiences a net force of F=PA.

3) A gas is characterized by three easily measured quantities: pressure P, volume V, and temperature T.

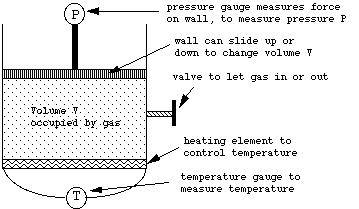
Suppose we had an apparatus that could simultaneously measure the pressure P, volume V, and temperature T of a gas inside a container. We could imagine such a device as shown below (see the text's discussion on page 112 of the "constant volume thermometer" for a more realistic such experimental device).

By adjusting the position of the moveable top wall, we can set the volume to whatever we wish. By measuring the force on this moveable wall we can measure the pressure. By adjusting the heating element on the bottom we can set the temperature to whatever we wish. By transferring gas into or out of the container via the valve on the side, we can change the amount of gas in the container.

The temperature gauge will measure temperature using the Celsius or centigrade scale (in use almost everywhere in the world except in the US), in which the freezing of water at the surface of the Earth (i.e. at "atmospheric" pressure) occurs at T = 0°C, and the boiling of water occurs at T = 100°C.

Experiment #1:

Imagine keeping the volume V and the amount of gas in the container fixed, while the temperature T is changed. Changing T will produce a change in pressure P. One could plot the resulting P for each value of T on a graph. One would find the result as shown below.

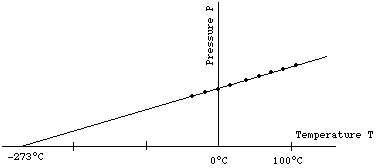
One sees the following two features: All the data points lie on a straight line. If one extrapolates this straight line back to P=0, it intersects the T axis at the value T = -273°C.

If one now either changes the amount of gas in the container or changes the type of gas (for example replaces nitrogen by oxygen) and then repeats the experiment, one finds that the data will still lie on a straight line which extrapolates to P = 0 at T = -273°C. The only thing that changes in the above graph will be the slope of the line.

It is therefore convenient to introduce a new temperature scale, called the Kelvin scale and written °K, such that T°K = T°C + 273. The above graph then looks like

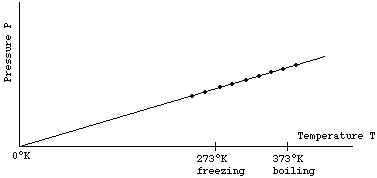
The above graph shows that, when T is measured with the Kelvin scale, the pressure P is proportional to the temperature T. If one doubles T, then P doubles. If one triples T, then P will triple, etc.

P ~ T       at constant V          (where we will use "~" to mean "proportional to")

0°K = -273°C is known as "absolute zero". If one could lower the temperature to absolute zero, the pressure of the ideal gas would be zero - the gas would exert no force on the walls of its container. We will see later that this would imply that the molecules that make up the gas have stopped moving! Since P cannot be negative, one can never decrease temperature below "absolute zero".

Experiment #2

Now imagine one keeps the pressure P and the amount of gas in the container fixed, while the temperature T is changed. One will find that as T is increased at constant P, the gas expands and moves the moveable wall, and the volume V will increase. One could plot the resulting V for each value of T on a graph. One would find the result as shown below.

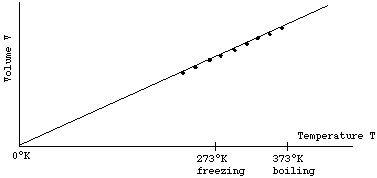
Again the data lies on a straight line that extrapolates back to V = 0 at T = 0°K. If one changes the amount or type of the gas, all that will change is the slope of the line. One concludes that for fixed pressure P, volume V is proportional to temperature T

V ~ T         at constant P

Combining the results of experiments #1 and #2 we can write

PV ~ T      or       

where for a fixed amount of a fixed type of gas, C remains a constant numerical value as either P, V, or T is changed.

Experiment #3

Now suppose one fixes the volume V and the temperature T, and opens the valve on the side of the container to add gas and double the amount of gas that was originally in the container. One will find that the pressure P doubles. If the amount of gas is tripled, P will triple, etc.

Similarly, if one fixes pressure P and temperature T, and doubles the amount of gas inside the container, then one finds that the volume V will double. If the amount of gas is tripled, then V will triple, etc.

Comparing these results with the result above, , one concludes that the constant C is proportional to the amount of gas in the container.

All the above is very interesting, but it does not yet indicate in any way that gases are made of tiny particles instead of being a continuous substance. Now we come to the crucial experiment!

Experiment #4

Imagine having two such containers as pictured above, each filled with a different pure gas. For example, let the first container be filled with hydrogen gas while the second is filled with oxygen gas. Measure the values of pressure P, volume V, and temperature T, of the hydrogen gas in the first container. Now adjust the pressure, volume and temperature of the oxygen gas in the second container to exactly the same values of P, V, and T as in the first container. This can be done in the following way: It is easy to fix V and T to be the same by adjusting the position of the moveable wall, and the temperature of the heating element. To make the pressure in the second container equal that of the first, one now opens the valve on the side and either lets gas in (to increase pressure) or lets gas out (to decrease pressure), until the desired pressure is achieved.

Now with the values of P, V, and T, adjusted to be the same in both containers, one measures the weight of the gas that is in each container (in practice, one should weigh first the empty container, and then weigh the container filled with the gas, and subtract the two to get the weight of the gas). If M_hydro is the total mass of the hydrogen gas in the first container, and M_oxy is the total mass of the oxygen gas in the second container, one will find the very surprising result that the ratio of these two masses is

      an integer!

Furthermore, this ratio will be independent of the particular values of P, V, and T that were used.

Similarly, if one repeated the above experiment using instead hydrogen gas and nitrogen gas, one would find for the mass ratio

       also an integer!

If one used nitrogen gas and oxygen gas one would find for the mass ratio

       a ratio of simple integers

If one used steam (water vapor) and hydrogen gas, one would find for the mass ratio

and so on. When subjected to equal values of P, V, and T, the ratio of total masses of all various types of gases always comes out to be the ratio of integers, and these integers do not depend on the particular values of P, V, and T used.

Since integers are associated with the counting of discrete objects, it is the observation of these integer mass ratios that suggests that the gasses are made up of discrete units, i.e. many tiny discrete particles. It is these integer mass ratios that give the evidence for an atomic theory of matter!

One can now explain the above findings by the following assumption: A pure gas (as opposed to a mixture of different types of gas) is made up of a certain number of identical tiny discrete particles, each particle having the same mass m. If N is the number of these gas particles in the container, then in our experimentally determined law , we should take the constant C to be proportional to the number of particles N. We can therefore write C = Nk_B, where the proportionality constant k_B is called "Boltzman's constant". Since we believe there should be a common equation that describes all gases, we assume k_B is a fundamental and universal constant of nature - it does not depend on either P, V, T, or N, or the type of gas being studied; it has the same value no matter where the experiment is being done, whether in Rochester, Tokyo, or on the moon. So our gas law becomes

or equivalently, 

The above result is known as the Ideal Gas Law.

If we now set up two containers, one with gas "a" and the other with gas "b", and we adjust the two containers to have exactly the same values of P, V, and T, then our gas law above tells us that the two gases must contain exactly the same number of particles N. The total mass of the first container will be M_a = m_aN, and the total mass of the second container will be M_b = m_bN, where m_a and m_b are the mass of one particle of gas "a" and one particle of gas "b" respectively. The ratio of the total masses is therefore

Thus the mass ratio depends only on which types of gas are being used, but is independent of the particular values of P, V, and T that were used.

This explains part of our observations, but does not yet explain why the ratio  is always the ratio of integers. We can explain this last fact by assuming that the particles of which each gas is made, are themselves made up of more fundamental basic building blocks. If the mass of this basic building block is , then if a particle of gas "a" is made up of an integer number  of these blocks, and a particle of gas "b" is made up of an integer number  of these blocks, then one would have  and , so that , which is now the ratio of two integers!

So our experiments lead to the conclusions that a gas is not a continuous substance, but is rather made up of many tiny discrete particles, and moreover, that these particles themselves are made up of a discrete number of a more basic building block. We now know that the particles of the gas are either atoms (if it is a pure elemental gas) or molecules. Molecules are made of atoms, and the mass of an atom consists almost entirely of the mass of an integer number of protons and neutrons that are found in the nucleus of the atom. The protons and neutrons are thus the basic building blocks referred to above, and it is known that the mass of a proton is essentially the same as the mass of a neutron, which we can take as the  in the above discussion.

When the chemists figured out the ideal gas law, and that the mass ratios of gases are always the ratios of integers, they called the basic building block one "atomic mass unit" abbreviated "amu". One can then find the mass, or also called the "atomic weight", of the basic elements, relative to the weight of a standard reference element. If we call the weight of the lightest element hydrogen 1 amu, then we have for the masses of other elements (an element is a substance made entirely out of one type of atom only):

element        chemical symbol        atomic weight

hydrogen         H                                  1 amu

helium             He                                4 amu

carbon             C                                 12 amu

nitrogen          N                                 14 amu

oxygen            O                                 16 amu

etc.

In this manner, chemists figured out the atomic weights of all the known elements, and constructed the periodic table. It was found that the properties of different elements changed in a periodic fashion, according to the integer value of their atomic weight. Understanding these periodicities is what lead to the development of atomic physics!

(In practice, the weights turn out not to be exactly pure integers, but only very very close to integers. This is because certain atoms can exist in both a normal form, and in an isotope form which has one additional neutron. In a typical sample of the gas, the fraction of atoms which are in the isotope form is extremely small, but their presence, averaged in with the normal atoms, leads to an average mass which is just a very slight amount off from an integer number of amu. Also, for historical reasons, carbon and not hydrogen was chosen as the standard reference element, so carbon is defined to have a mass of exactly 12 amu, while the other elements mass is determined relative to that of carbon).

Similarly, one can determine the "molecular weight" of gases whose basic particles are molecules. It is now known, for example, that many of the most common elemental gases, such as hydrogen, oxygen, and nitrogen, consist of molecules made up of two atoms each. For example the particles of hydrogen gas are not atoms of hydrogen H, but rather molecules of hydrogen H₂, where the symbol means there are 2 atoms of H in each molecule. The molecular weights of some of these gases are:

gas                      chemical symbol               molecular weight

hydrogen                   H₂                                                    2 amu

nitrogen                     N₂                                                    28 amu

oxygen                      O₂                                                    32 amu

steam                        H₂O                                                 2+16 = 18 amu

carbon monoxide      CO                                                 12+16 = 28 amu

carbon dioxide          CO₂                                               12+(2)(16) = 44 amu

etc.

A terminology introduced by the chemists, is the concept of the mole. If one takes an amount of a substance, such that its mass as measured in grams is equal to the numerical value of its mass in amu, then this amount is called one "gram molecular weight" or one "mole" of the substance. For example, 32 grams of oxygen gas O₂ is one mole of oxygen gas. 44 grams of carbon dioxide CO₂ is one mole of carbon dioxide CO₂.  18 grams of water is one mole of water H₂O.

One can now use the ideal gas law to determine the chemical formula of molecules. For example, if one wants to make water from hydrogen and oxygen gas, one would discover that it takes exactly twice as many molecules of H₂ gas to combine with a given number of molecules of O₂ gas, to create the steam, leaving none of the initial hydrogen and oxygen left over. For example, if we had a container of O₂ at fixed values of P, V, and T, we would have to combine it with a container of H₂ at the same values of P and T but twice the volume. This implies that if there are N molecules of oxygen, one needs 2N molecules of hydrogen to create the steam with no left over O₂ or H₂. One could then measure the P, V, and T of the resulting steam and find that the combination of PV/T for the steam was the same value as was the initial PV/T for the hydrogen gas. This implies that the number of molecules of steam that have been created, is exactly the same as the number of molecules of hydrogen that were used, ie. 2N. The conclusion is that the steam must be made up of molecules of H₂O, and not for example H₄O₂

2N(H₂) + N(O₂) --> 2N(H₂O)

If water was made of molecules of H₄O₂, we would find only N such molecules after the reaction: 2N(H2) + N(O₂) --> N(H₄O₂). But this is not what happens.

In this way, one can find out the relative weights of molecular gases in amu, as well as their molecular formulae.

Since the number of amu of a molecular weight of a given substance reflects the weight of one single atom or one single molecule of the substance, it must be true that one mole of any pure substance (ie. a substance made up of all the same type of molecule or atom) contains the same number of particles (ie. molecules or atoms) as one mole of any other pure substance. The number of particles (atoms or molecules) in one mole of a substance is called Avogadro's number of particles, and is denoted by the symbol N_A.

In chemistry, one usually encounters the ideal gas law in the form

PV = nRT

where n is the number of moles of the gas, and R is called the universal gas constant. Comparing the above to PV = Nk_BT, and noting that n moles contains nN_A molecules of the gas, we conclude that

N_Ak_B = R          gives the relation between R and k_B.

R is easily measured, since one can easily weigh the gas and find the number of moles that one has. One finds R = 8.3 j/°K, where "j" stands for "joules", the unit of energy.

To understand the units of R, note that since P is force per area, or force per length squared, and V is length cubed, PV is force times length - this is the unit of the left hand side of the above equation.

units of PV are nt m, but nt = kg m/s² so nt m = (kg m/s²)(m) = kg m²/s² = kg (m/s)²

The last term in the above has the same units as mass time velocity squared, but this is the units of kinetic energy , so PV has the units of energy. The units of energy are therefore:

unit of energy, the joule,       j = nt m = kg m²/s²

So finally, if nRT has units of energy, and n the number of moles is dimensionaless, then R has the units of energy per degree K.

Since R is readily measurable, if one could measure Avogadro's number N_A, one could then determine Boltman's constant k_B = R/N_A, and so be able to explicitly measure the number of molecules N in a given quantity of gas! By measuring the P, V, and T of the gas, one would find

Measuring the total mass in grams of the gas in the container, M, one could then determine the mass in grams of one single molecule of the gas!
m = M/N.

To determine Avogardo's number N_A, one could imagine doing the following conceptual experiment (for a discussion of a more realistic laboratory version of this experiment, see the text, problem 4, page 118).

Imagine that a molecule of oil has a size of length "a". Pour out a given amount of this liquid oil on the surface of water. For a properly chosen oil, it will spread out on the surface of the water forming a patch of one molecular layer in thickness. If there are N molecules of oil, then the area of this patch of oil would be A = Na². If the volume of oil poured out was originally V, then we also have that V = Na³. The ratio then gives the molecule size a, and we can also get the number of molecules N, as follows:

If we further knew the chemical formula of the oil molecules, we could first weigh the oil and determine that we had some fraction f of one mole of oil, and so N = fN_A. Since we can directly measure f, A, and V, we now combine these facts as follows:

determines N_A in terms of the measured f, A, and V. One finds for Avogadro's number,

molecules per mole.

We can now determine the weight of one atom of hydrogen. The atomic weight of hydrogen is 1.0079 amu. N_A atoms of hydrogen therefore weigh 1.0079 grams. We therefore can conclude that one atom of hydrogen weighs exactly (1.0079)/(6.02 x 10²³) = 1.67 x 10^-24 grams!

Boltzman's constant is

Atmoshperic pressure:

Pressure P is a force per unit area, so it has units of nt/m² = (kg m/s²)/(m²) = kg/(m s²)

This unit is called the "Pascal", abbreviated "Pa"

1 Pa = 1 kg/(m s²)

Atmospheric pressure is, in English units, 14.7 lb/inch², where to convert to MKS units, we have 1 lb = 4.448 nt, and 1 inch = 2.54 cm = 0.0254 m.

(note that pounds "lb" is a unit of force, not a unit of mass. In the English system of units, the unit of mass is called the "slug", where 1 lb = (1 slug)(g), where g = 32.2 ft/s² is the gravitational acceleration in English units.)

So 1 lb/inch² = (4.448 nt)/(0.0254 m)² = 6.892 x 10³ nt/m² = 6.892 x 10³ Pa

Atmospheric pressure,

1 atm = (14.7)(6.892 x 10³ Pa) = 1.013 x 10⁵ Pa

Volume of one mole of gas

What volume does one mole of any gas occupy, at room temperature and pressure?

Ideal gas law is PV = nRT. Using n=1 mole, T=293°K at room temperature, and  1 atm = 1.013 x 105 Pa, we get,

V = nRT/P = (1)(8.3 j/°K)(293°K)/(1.013 x 105 nt/m²)

= 0.024 m3 where we used j = nt m so that j/(nt/m²)=m³

= 24 x 10^-3 m³ use 10^-3 m3 = 1 liter

= 24 liters

One mole of gas occupies a volume of 24 liters. If repeat this calculation at 273°K, i.e. at the freezing temperature of water, one finds V = 22.4 liters.

Density of an ideal gas

The idea gas law is PV = Nk_BT

The particle density is N/V

So the density is N/V = P/(k_BT)

Any two gases at the same temperature and pressure have the same density of particles.

What is the density at atmospheric pressure and room temperature?

Using P = 1.013 x 10⁵ Pa, T = 293°K, and k_B = 1.38 x 10^-23 j/°K, we get

N/V = (1.013 x 10⁵ Pa)/(1.38 x 10^-23 x 293 j) = 0.25 x 10²⁶ m^-3

Volume per particle is V/N = 4 x 10^-26 m³

Average spacing between particles is

Compare this to our earlier calculation of the spacing between molecules of water where we found L ~ 3 Angstrom.