In the preceding section we discussed the derivation of the Ideal Gas Law from an experimental point of view. We now want to develop a theoretical derivation of the Ideal Gas Law, based on our microscopic picture of molecules in motion in a gas, combined with Newton's Laws.

We start with the following assumptions about the motion of molecules in an ideal gas:

(i) The average kinetic energy of a molecule is very much larger than its gravitational potential energy, so that the effects of gravity can be considered negligible (in an example later in this section, we will discuss what happens when this is not the case).

(ii) The interactions between molecules are very weak, so that they do not influence each others motion except when they come close to each other on the length scale of the size of a molecule. In other words, we can regard the molecules as billiard balls, which interact with each other only when they have a head on collision. The effect of such collisions is to send each molecule off in a random direction.

(iii) The density of molecules is very dilute, so that the average spacing between molecules is much larger than the average size of one molecule. The molecules motion can therefore be viewed as long segments of motion with a constant velocity, in-between any two successive collisions with other molecules, i.e. the molecule is taking a random walk. In the last section, we saw that the average spaceing between molecules in an ideal gas was about 34 Angstrom, while the typical size of a molecule is a few Angstrom. So this is a pretty good approximation.

We now want to show that the pressure that such an ideal gas exerts on the wall of a container, is due to the collisions which the molecules experience with the wall.

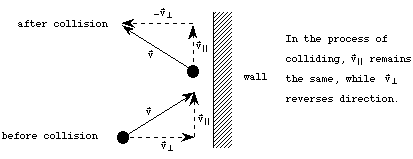
Consider a molecule which is traveling towards the wall, collides with the wall, and is reflected backwards. Imagine that the wall is perfectly flat and rigid. In this case, since the wall absorbs no energy from the collision, the molecules kinetic energy must be the same before and after the collision. The component of the molecule's velocity which is parallel to the wall will remain unchanged, while the component perpendicular to the wall will reverse direction, as shown in the picture below.

The change in the molecules velocity as a result of the collision is therefore

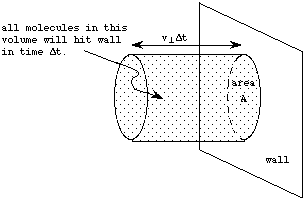
Now consider all such molecules which are traveling towards the wall with a perpendicular component of their velocity . Let us find the average number of collisions per unit time, that such molecules make with the wall. Consider a time interval . Any such molecule that is within a distance  of the wall will reach the wall and collide with it within the time . If we consider a piece of the wall of area A, then the number of such molecules that collide with this piece of the wall in the time  is therefore  where  is defined as the number of molecules per unit volume with perpendicular velocity of magnitude  (see picture below). The factor  is because of all the molecules with perpendicular velocity of magnitude , only half are moving towards the wall; the other half are moving away from the wall.

If we call the average time between collisions with the wall of such molecules , then the average number of collisions per unit time, , is just the number of collisions  within time , divided by the time interval . We therefore have

Now when each molecule collides with the wall, it experiences a change in velocity . This change in velocity is equivalent to an acceleration of the gas. The average acceleration that the gas experiences is therefore the change in velocity per collision, times the number of collisions per unit time

If we multiply the above by the mass of each molecule M, we get from Newton's second law the average force that the piece of the wall is exerting on the gas

The minus sign indicates that this force is pointing perpendicular to the wall inwards into the gas. Now by Newton's third law, the gas must be exerting a force on the wall equal in magnitude and opposite in direction. So the force on the wall is pointing perpendicular to the wall, directed outwards from the gas, and it has a magnitude

This is the force due to those molecules which were moving with the particular perpendicular velocity . To get the total force, we should add the forces from all molecules moving with different values of . We can now write , where n is the density of all molecules per unit volume, and  is the probability that any molecule chosen at random will have velocity with magnitude . Summing over all values of , we get for the total force

where  is just the average value of , averaged over all molecules in the gas. The pressure is now this force divided by the area A, so

Now, since all three directions in space are the same to molecules in the gas, we expect that the average velocity squared in any one direction is just equal to (1/3) the total average velocity squared. In more detail:

where we take x and y as the two directions parallel to the plane of the wall, and the above is just the three dimensional analog of Pythagorous' theorem.

So

since all directions look the same. So

So finally we get

Now note that the density of particles can be written as n=N/V where N is the total number of particles, and V is the volume occupied by the gas. We therefore have

The above is just equal to the ideal gas law, PV = Nk_BT, provided we identify the temperature as

where  is the average kinetic energy of a molecule in the gas! Thus the average kinetic energy of a gas molecule is related to temperature by

This result relates the thermodynamic quantity, temperature, to the microscopic quantity, the average kinetic energy of the molecules.

Note that in the above derivation, we assumed that the number of molecules with velocity  was given by , where n is the density of all molecules per unit volume, and  is the probability that any molecule chosen at random will have velocity with magnitude . This is equivalent to the assumption that if  is the average kinetic energy expected for one molecule chosen at random, then the total kinetic energy of the gas will be exactly . For any given sample of gas with N molecules contained in a volume V, this is not exactly true. Just as in 10 flips of a coin, it is not necessarily true that there will be exactly 5 = (10)(1/2) heads, so in a given sample of gas of N molecules, it is not necessarily true that the total kinetic energy is exactly . However we know the likely range for the total kinetic energy from our discussion of the normal distribution in the early part of the course! If  is the standard deviation of the kinetic energy of a single molecule drawn at random, than the standard deviation of the total kinetic energy of N molecules is . To 99.99% accuracy, the total kinetic energy of a gas of N molecules will be found within the range . The kinetic energy per molecule will be the total kinetic energy divided by N, i.e. . If N is small, the variation about the mean  can be substantial. However as N gets big, the range decreases proportional to . For , the typical number of molecules in a gas, the term  is so small that it is completely negligible compared to the mean . Thus the error associated with replacing the behavior of any given sample of N gas molecules with the behavior of the average, is completely negligible because N is so large. This is exactly why it is possible to describe the gas by the variable "temperature", which measures the average kinetic energy, and not worry at all about the details of what each individual molecule is doing, or worry about the possibility that any given sample of gas is different than the average.

Average molecular speed at room temperature

We can now go back to our experiment of the ink particle diffusing in the water, and understand why its speed in between collisions was so large. According to the above

and so the root mean square average speed of the molecule in between collisions is

Suppose that one molecule of ink has a molecular weight of order 50 amu. Then its mass is 50 times the mass of a hydrogen atom, so

where we used that . At room temperature T=293°K (68°F) using , we get for the root mean square average speed of the ink molecule

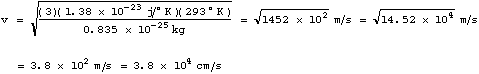
where we used .

Compare this to the result we found when we did our ink diffusion experiment, . Given the crudeness of our experiment, this rough agreement is quite impressive.

We see that it is the temperature of the gas that determines the average speed of the molecules v. If one increases T, v will grow proportional to the square root of T. Since the diffusion constant of the ink particles was  (where L is the average distance traveled between two successive collisions, and  is the average time between two successive collisions, and so ), we can increase D and make the ink diffuse faster by heating the water!
 
 

How high is the sky?

In our above discussion about the motion of molecules in a gas, we ignored any effects due to the force of gravity acting on the molecules. This is generally a very good approximation as long as we are considering gases confined to containers inside our laboratory. To see that this is so, consider how much energy it takes to lift a molecule of air from the bottom to the top of a container 1 meter high. This energy is just the difference in gravitational potential energy between the bottom and the top of the container. If we set our scale so that the bottom of the container is at height zero, and the top of the container is at height , the change in potential energy is just,

Ordinary air is made up mostly of nitrogen molecules , each of which weighs (2)(14)=28 amu. Since one amu weighs , the mass M in the above equation is,

The energy needed to move the molecule from the top to the bottom of the container is then,

Compare this to the average kinetic energy of the molecule at room temperature,

The ratio of the two is,

So the energy needed to move against the force of gravity is a very small fraction of the kinetic energy of the molecule. If the molecule converted  of its kinetic energy into potential energy by moving from the bottom to the top of the container, the molecule's kinetic energy, and hence its speed, would not noticeably change at all. This is why we could ignore the effects of gravity.

Now, however, consider the atmosphere surrounding the earth. If a gas expands to fill all of the space available to it, what keeps the atmosphere from expanding to fill up all of outer space? The answer is the gravitational force of the earth on the molecules in the atmosphere. For the atmosphere, ignoring the effects of gravity on the molecules is clearly an inadequate approximation. In other words, when we consider the atmosphere, the "container" that holds the gas is now so big that our earlier arguement will fail.

Let us now therefore compute how tall a container has to be for the change in gravitational potential energy between top and bottom to be equal to the average kinetic energy of a molecule. Under such a situation, the gravitational force can certainly not be neglected. The length scale we compute this way (i.e. the height of the container) then gives a measure of the length scale over which the atmospheric density decreases as you go above the surface of the earth.

Before we start, we can already know what length we are looking to get. If you go in an airplane flying at a typical height of 30,000 ft, you know that the cabin is pressurized. If the cabin should have a leak to the outside, the oxygen masks will fall from the overhead cabinets and you would be advised to put them on! The is because at this height, the density and pressure of the air is sufficiently small compared to that on earth, that you will have a hard time breathing without the mask. Similarly, on top of Mt. Everest (about 5.5 miles high), you need an oxygen mask to breath. The heights involved are on the order of 5 miles high. So the length we are looking for, on which the effects of gravity must be including in considering the behavior of a gas, is a length of the order of a few miles.

Now for calculation. We want  so big that,

So,

To convert this to miles, use 

So,

So we find that the relevant length for the effects of gravity to be important in considering the atmosphere of the earth is about 8 miles! This is close to what we expected from considering the height of flying jet airplanes, and the height of Mt. Everest.

One can show with a more detailed calculation that, assuming the atmosphere is at a constant temperature (not a bad approximation as long as one doesn't go too high), the pressure and the density of the atmosphere decreases by half for roughly every 4 miles you increase in height.