Mean and Standard Deviation
When we discussed the probability distribution for flipping n heads in N trials, we introduced the notion of the "average" and the "width". The average was the most likely outcome, where the distribution had its maximum value. The width was a measure of how spread out the probability distribution was about the average. We now want to give a more precise mathematical definition of these concepts.
As an example, consider a class of 10 students taking an exam, and getting the following 10 grades: 60, 60, 70, 70, 70, 80, 80, 80, 90, 90. What is the average grade on the exam? The natural way to define this average is to add all the grades up and divide by the number of students:
average = ![]() = 75
= 75
Since each grade is obtained by more than just one student, we could shorten the calculation of the numerator by adding up each different grade multiplied by the number of students who got that grade:
average = ![]() = 75
= 75
We could now rearrange the above calculation as follows:
average = ![]() = 75
= 75
The above represents the sum of each grade multiplied by the fraction of students that got that grade.
Now if the class is very large (much bigger than 10) and is filled with only "typical" students, we could say that the fraction of students receiving a given grade is equal to the probability that a typical student will receive that grade. The above average then represents the sum of all grades multiplied by the probability that a typical student will get that grade. This then motivates our definition for the average of any probability distribution.
Definition of the mean or average:
Suppose we have an experiment with outcomes that can be labeled by the integers r=0,1,2,...,N. The probability for outcome r is P(r). Suppose that to each outcome r is associated a numerical value x
r, i.e. x0 is the value of outcome 0, x1 is the value of outcome 1, etc. Then the average, or mean, value of x, denoted by the symbol <x>, is defined by,![]()
The mean value of x is also sometimes denoted by the symbol
µ when it is understood what property "x" is being measured (this is the notation that the text follows). Or, we might write µx to indicate that it is the "average of x" that we are talking about. We will use <x> and µ interchangeably, according to which is more convenient.We can also consider the average of any function f(x) of the values x
r by defining,![]()
For example, if P(x) is the probability to find exactly x heads in N flips of a fair coin, we can associate with each outcome the numerical value x, i.e. the number of heads found. The average number of heads found in N flips is then,
![]()
Suppose now one is playing a betting game in which for each head flipped one wins $10 and for each tail flipped one loses $10. If x heads are found in N flips, there must be N-x tails, so for x heads in N flips the net winning is given by the function f(x) = 10x-10(N-x) = 10(2x-N) dollars. The average amount in dollars that is won in a game of N flips is then,
![]()
Using the definition of <x> above, you should convince yourself that the following result is true. If a, b and c are three constant numbers, then,
![]()
Standard Deviation
We now want to define a quantity that will tell us how spread out the probability distribution is about the average value, and thus give us some measure of the "width". Going back to our example of grades on a test, one guess would be to compute the difference of each grade from the average, sum these up for all the grades, and divide by the number of students. This would give,
![]()
= ![]() = 0.
= 0.
This comes out to zero, since the way the average was defined guarantees that the grades below the average are exactly compensated by the grades above the average.
So the above is not a good measure of the width of the probability distribution! One way around this problem of the cancellation of outcomes below the average against outcomes above the average, is to use the square of the difference of each grade from the average. Since the square of a number is always positive, regardless of whether the number itself is positive or negative, there can be no cancellation of terms. We therefore compute for our example of exam grades:
![]()
= ![]()
= ![]() =
= ![]() = 105
= 105
The above is just the average value of the square of the deviation
from the average grade. To get a measure of the deviation from the
average grade, we should now take the square root of this number. This
procedure then defines the root mean square deviation also called
the standard deviation. For our exam grades example the standard
deviation is therefore, ![]() =
10.25.
=
10.25.
This tells us, in a way we will be more precise about later, that most of the grades occur between 75+10.25 = 85.25 and 75-10.25 = 64.75.
For a general probability distribution P(r) the standard deviation is denoted by the symbol
![]()
Note that if we define the function ![]() ,
then the above expression is just the definition for the
average value of <f(x)>. So we have that
,
then the above expression is just the definition for the
average value of <f(x)>. So we have that
![]()
The square of the standard deviation is just the average value of the deviation from the average squared.
An Alternative Formula for Computing Standard Deviation
Here we derive an alternative, and often easier, formula for
calculating the standard deviation ![]() . Our earlier definition
was,
. Our earlier definition
was,
![]()
Expanding out the square we get,
![]()
In computing the average above that defines
to rewrite the above as:
![]()
(where we made the identifications a=1, b=
![]()
So we finally get our new alternative formular for the standard deviation,
![]()
The standard deviation squared is equal to the "average of the square of x" minus the "square of the average of x".
Note the very important fact that
This is a point of common confusion, so be careful that you understand this! From our definition of average we have,
![]()
while
![]()
The two expressions are not the same, and in general they are not equal!
(To see that they are not the same, just expand the square in the second equation.)
Example
What is the mean and standard deviation for the number of heads obtained in one flip of one coin? We will denote these by
First we compute the average
There are only two outcomes, corresponding to x=0 heads or x=1 head. The probability to get 0 heads (i.e. a tail) is P(0)=1/2, and the probability to get 1 head is P(1)=1/2. The mean is therefore,
![]()
To get the standard deviation, we will do it two ways, using both the
formulars we derived.
Method 1:
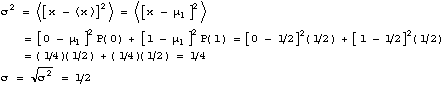
Method 2
:![]()
Compute:
![]()
![]()
So,
![]()
Both formulars give the same answer.
For a general two outcome experiment with probability P(1)=p for a "win" and
P(0)=(1-p) for a "lose", the mean number of wins x in one trial of the experiment is:
![]()
Hence the mean number of wins in one trial is just the probability that the one trial results in a win!
The standard deviation is (lets use Method 2),
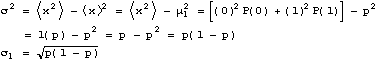
These results for