Average of the Sum of Two Independent Random Experimeints
We next consider the following very important problem:
Suppose one has two different, independent random experiments. The outcomes of experiment #1 can be labeled by the integers 1, 2, ..., N, and have probabilities P(1), P(2), ..., P(N) of occuring. The numerical values associated with these outcomes are,
For the purpose of making the algebra simple, we will consider the specific case where the first experiment has only N=2 outcomes, and the second experiment has only M=3 outcomes. However the steps we will make are easily extended to the general case.
The outcomes of experiment #1 are:
The outcomes of experiment #2 are:
We can label the outcomes of doing both experiments by the pair of numbers (x,y). In our example, there are (N)(M) = (2)(3) = 6 possible outcomes, which are:
![]()
and these have associated with them the numerical values:
![]()
What are the probabilities for each of the above 6 outcomes? Here we use the fact that the two experiments are independent, i.e. the outcome of one has no effect on the outcome of the other. Hence, the probability to get outcome (x,y) is just the product P(x)P'(y). We can now compute the average
![]()
Expand out the factors and regroup common terms to get,
![]()
Now, each term in a square bracket just sums to unity! This is because
![]()
If we look at the first two terms on the left hand side, we see that they are just the definition of the average of x,
or in our alternate notation,
The average of the sum is equal to the sum of the averages! This result is true in general for any values of N and M. For the above result to be true, it is crucial that the two experiments are independent of each other.
Standard Deviation for the Sum of Two Independent Random Experiments
Next, we want to know what is the standard deviation of the outcome of doing the two experiments? Again, we consider the simple case where N=2 and M=3. Using method 2 for computing standard deviation, we have,
![]()
Expanding out the square in the first term, and applying our result
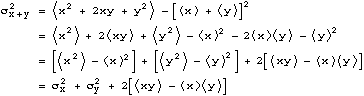
Let us consider the last term on the right hand side. We can compute this average value by suming over the 6 possible outcomes (x,y). We get,
![]()
After some staring at the above expression, one realized that it can be factored as below,
![]()
(You can expand the above, multiplying out the factors, to check that this is so). Now the first term on the right hand side is just the definition of
![]()
(Note: this result is true only in the case that x and y are independent, i.e. prob(x,y)=P(x)P'(y)). Using this result, we see that the last term in our expression for
![]()
The square of the standard deviation of the sum, is equal to the sum of the squares of the standard deviations.
Example
What is the average and standard deviation of the number of heads found in two flips of a coin? Assume that the probability of a head is p (for a fair coin, p=1/2; for a loaded coin p might be something else).
We will use our results above. Let x be the number of heads found on the first flip, and y the number of heads found on the second flip. We then have,
![]()
But in this example, the two experiments are the same physical process -- they therefore have the same probabilities and average values. We already found that the average number of heads found in one flip of a coin was
![]()
If we denote
![]()
For the standard deviation we apply,
![]()
Here, we have ,
![]()
where we earlier found that
![]()
or,
![]()
Thus, when we go from one to two flips, the average increased by a factor 2, but the standard deviation only increased by a factor
![]()