We come now to our first real application of the ideas of probability to an interesting physical phenomenon, the process of diffusion.

If we throw a ball, then after the ball leaves our hand the horizontal distance x that it travels in time t is given by

x = vt

where v is the horizontal speed with which the ball leaves our hand. Thus the distance the ball travels is proportional to the time it is traveling. We will now see that for a particle undergoing diffusive motion, there is a very different relationship between the distance and the time of travel.

We start with the following example. Suppose a physicist has been too long at the local bar and has had too much to drink. He leaves the bar and starts to walk home. However he can no longer remember the way and so after each step he flips a fair coin to determine the direction of his next step: if heads he goes forward a distance +L, if tails he goes backwards a distance -L. Such a process is known, for obvious reasons, as a "random walk".

We are now interested to know how far the physicist is likely to have wandered from his starting point, after taking N steps. Or alternatively, if he lives a distance d from the bar, home many steps N does he need to take to find his way home?

Let us start by computing the probability  that the physicist has traveled exactly the distance x after taking exactly N steps (x will be positive for a net forward motion, and negative for a net backwards motion).

We can relate the position of the physicist x to the number of heads n he flips in making the N steps. If he flips n heads, he has taken n steps forward, each of distance +L. However he has also gotten N-n tails, and so has taken N-n steps backwards, each of distance -L. The net distance he has traveled is therefore,

What is the probability that in the N flips he has gotten n heads? This is just the binomial distribution,

             for a fair coin with p=1/2.

So to plot the probability  that the physicist has traveled a distance x, all we need to do is to make a table, indicating the number of heads n, the probability to get that number of heads , and the position x one reaches if one got that number of heads (note: I put the bar over  so you do not confuse it with the notation for the binomial distribution ):

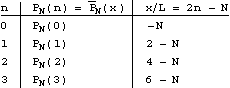
and so on, for n = 0 all the way up to n = N. From the last two columns we can then plot  vs. x, which I show below for N = 10, 40, and 160 steps.

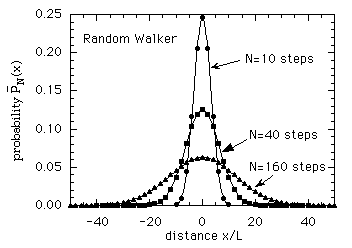
We can observe the following features in the plots above. In each case, the peak of the probability distribution remains at the starting position x=0, and the distributions are symmetric about x=0. This is because on average he is just as likely to go the distance +x forward, as to go the distance -x backwards. We therefore expect that the average distance traveled will always remain zero. However, as the number of steps N increases, the width of the distribution increases, and so as N grows there is a growing probability that the random walker will be found farther and farther from the starting point. From the graph we can see that when N increases a factor of 4, the width increases a factor of 2. This is just the rule we learned for the standard deviation. Note also that as N increases a factor 4, the height of the peak at x=0 decreases a factor 2. This is because the area under the curve is just the total probability, which must always equal unity -- so as the width doubles, the height must half, so that the area remains constant.

It should be clear from the above graphs that the "typical" distance the walker is likely to have traveled from the starting point is related to the width, or equivalently the standard deviation, of the distribution. So let us now compute the average and the standard deviation of the distance traveled after N steps.

The total distance traveled x, is just the sum of the distances traveled on each step of the walk. If  is the distance traveled on step number i, then we have,

Now since the random process involved in taking each step is the same, and each step  is independent of all the others, we can apply our results for computing the average and standard deviation of the sum of N identical independent random variables:

where  and  are just the average and standard deviation of the distance traveled in a single step. We can compute these as follows, using our general rules. In a single step, there are only two outcomes, +L and -L, each of which happens with probability 1/2. Therefore,

So,

Combining these results we get,

Thus, as expected, the average distance traveled is always zero, while the standard deviation increases as the square root of the number of steps. Because the average is always zero, the standard deviation is also the "root mean square" average distance traveled. We can therefore write,

,       or,       

Suppose that the time the walker takes between steps is  seconds ( is the Greek letter "tau"). Then the number of steps N taken in time t seconds is . We can then write the above as,

It is customary to give the last term in parenthesis a name: the diffusion coefficeint D,

, where L is the distance traveled in one step of time .

If we define  as the average speed of the random walker in a single step, we can also write,

The equation for the mean square distance traveled is then,

               with the average distance being given by           

Any object whose displacement is described by the above two equations is said to be undergoing diffusive motion.

Note the very different behavior of diffusive motion as compared to the more familiar motion at constant speed. In the latter case, x = vt, and the distance traveled grows proportionate to the time traveled. In diffusive motion it is the mean square displacement  that grows proportionate to the time traveled, so the root mean square distance traveled  grows only as the square root of the time traveled. In diffusive motion, the typical distance traveled thus grows much more slowly with time as compared to motion at constant speed. The reason that diffusion is so much slower than motion with a constant speed is because in diffusion, although the speed  of each single step remains constant, the direction is changing randomly at each step.

Let us now return to our original question. If the physicist lives a distance d from the bar, how many steps does he need to take in order to find home?

As a rough answer we can say that he should take N steps such that the root mean square distance traveled is equal to d, or,

Finally, suppose we had a large number M of particles, all taking independent random walks, and all starting at the same initial position. At N=0 steps, they are all concentrated at position x=0. After N steps, how many of the particles will be at position x?

Since the probability for a single particle to be at x after N steps is , the average number of walkers that will be found at x is . Thus the concentration of particles spreads out from the origin as N increases, according to how the probability distribution  spreads with increasing N. This spreading is given by , and hence .

An example of the above is when you place a drop of ink in water. If you do this you will see the drop spread out, growing in radius as time increases. If you measure this growth, you will see that the spreading drop grows proportionate to . This dependence indicates that the ink is diffusing into the water. From the above discussion, we see that diffusion results when the individual particles that make up something are all taking independent random walks. That ink diffuses into water is therefore a good demonstration of the atomic theory of matter! The ink and the water are both made up of tiny particles. The collisions between these particles result in their taking random walks. The growth of the ink spot with time as  is then a consequence of this random motion!