The modern atomic theory of gases tells us that a gas is made up of many small particles (atoms or molecules) such that the particles are spaced far apart from each other on the length scale of the size of the particles. We can imagine the following simple model for the behavior of these particles, which is not too far from the truth. Each particle of the gas is undergoing a random motion as follows: it moves with a constant speed  in a given direction, until it collides with another particle, after which it bounces off with speed  in a new random direction. How fast are these particles in a gas moving? How big is the speed ?

To answer this question, we can view the motion of the particle in the above model, as if it is taking a random walk. The distance L of the steps in the walk is just the distance the particle travels inbetween two sucessive collisions. The time  is just the time inbetween two sucessive collisions. If the speed inbetween collisions is , then L and  are related by , or equivalently . The diffusion constant for the particles of the gas is therefore:

If me measure D in an experiment, and if we know L, then we can use the above result to calculate the speed  of the atomic or molecular particles of the gas.

Instead of trying to measure the diffusion constant of a molecule in a gas, we do instead the following simpler experiment in lecture. A simple example of diffusion is to place a drop of dark blue ink in a bowl of water. Initially the ink is all concentrated near one position. As time increases, one sees the spot spread out and get fainter, until after a sufficiently long time, the entire bowl of water is a uniform light pale blue. The decrease in the intensity of the color of the spot, from an initial dark blue to a final very light pale blue, is a result of the decreasing concentration of ink as it diffuses into the water. If one measured the spreading of the spot, one would find that it grows in time like . The particles of ink are taking a random walk as they collide with the water molecules.

Note that the fact that the ink does indeed diffuse into the water is itself suggestive evidence that the ink and the water are both indeed made of many tiny particles which are colliding and so undergoing random walks. This is far from obvious; when one first looks at water or ink, they look like smooth continuous substances rather being made up of discrete small particles. Without any microscope to directly see the particles, the observation of diffusion gives suggestive evidence for the atomistic nature of matter!

In our experiment in class, we found that the ink spread out approximately 1/4 inch in 2 minutes. This gives a diffusion constant of

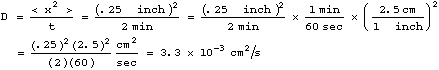
where we have used the facts that there are 60 seconds in one minute, and 2.5 centimeters in one inch, to convert the units of D from square inches per minute to square centimeters per second (). The later units are those most commonly used in physics.

We now want to use our measured value of D to determine the speed v of the ink particles, as the travel inbetween collisions with the water molecules. Since D=Lv_o, we still need to determine L, the distance traveled between collisions. We will make the reasonable assumption that the distance between collisions is just the average distance between water molecules.

If you remember your elementary chemistry or physics, you should recall that the length of typical atomic distances is the "Angstrom", denoted by the symbol Å, and having the value, Å=. So we could guess that the distance between water molecules L should be a few Å. If you remember even more of your elementary chemistry, we can get a better estimate for L by the argument below:

If one has a volume V filled with N molecules of water, then the density of molecules per unit volume is  ( is Greek letter "rho"). The amount of volume per molecule is then . If L is the separation between water molecules, then this volume per molecule is just . So combining these results we conclude that , or . So if we know the density of water molecules , we can find L.

Now from elementary chemisty (we will review this later, if you don't remember it now) we know that one "gram molecular weight" of water, , weighs 18 grams. One gram molecular weight of something contains one Avogradro's number,  of molecules of the stuff. So there are  molecules of water in 18 grams of water, or  molecules in one gram of water. Now 1 gram of water at room temperature occupies  of volume. So  of water contains  molecules, giving a density of . The distance between collisions is therefore

Using our measured value of , and , we now use , or , to find the speed of the ink particles inbetween collisions,

To get a better idea of how fast this is, lets convert back to more familiar units:

so

Pretty fast!!

We can also now compute the collision time 

So the collision time is really short!

One of our goals towards the end of the course will be to understand why this speed  is so fast.
 
 

Some additional comments:

You could wonder how our simple random walk, where in each step we move only a fixed amount either forward or backward, could be a good model of random molecular collisions. Clearly the distance between collisions is not always exactly L, but only on average L. In each particular collisions the actual distance gone depends on the velocity of the molecule, and the velocity and positions of the nearby molecules - certainly a distributions of distances is possible. Suppose we describe this with a probability distribution P(x), the probability to go distance x between two successive collisions (x has positive sign for forward, negative sign for backward). Clearly the mean distance of the probability distribution P(x) is zero - on average the molecule goes just as much to the right as to the left. But P(x) has some non zero root mean square average (the standard deviation), which we will call L. Now the distance gone in N steps is just the result of adding the outcomes of the probability distribution P(x), N times. We know that the standard deviation of this sum of N elementary displacements is then just L. This is all we need to get diffusion - the details of the elementary displacement probability distribution P(x) don't really matter - only the root mean square average distance in one step L is important.

For our simple random walk in one dimension (a walk along a line) we saw that the probability to remain at the origin decreased with the number of steps as . This was a consequence of the width growing as . For a random walk in two dimensions, the width of the distribution grows like  in each of the two orthogonal directions. Thus the area over which a sizable probability gets spread out goes like . If the total amount of probability must always sum to unity, this suggests that the height of the peak of the probability distribution (which is the probability to remain at the origin) must decrease as 1/N. For a random walk in three dimensions, the probability gets spread out over a volume that grows like . So the height of the peak must decrease as .

Since in diffusion, the number of steps N is proportional to the time t, for a process in which diffusion is limited to one direction only, the concentration at the origin decreases in time as ; for a process in which diffusion takes place in two independent directions the concentration at the origin decreases in time a ; and for a process in which diffusion takes place in all three directions in space, the concentration decreases in time as .