We can also consider a random walk in which the probability to move in one direction is greater than the probability to move in the opposite direction. Suppose at each step the walker has a probability p to go forward, and a probability (1-p) to go backwards. This is binomial process with probability p. Then the average distance gone in one step is

The standard deviation squared of the distance gone in one step is

where

and

So

and

Alternatively, if we write the probability p in terms of its deviation from 1/2, i.e. , then we can rewrite the above results in terms of  which measures the deviation from an unbiased walk.

Setting  in the above gives back the results we found earlier for the unbiased random walk with p=1/2.

Now after N such steps, the mean distance gone is

and the standard deviation of the distance gone is

So when the walk is biased, with ,  is not zero; we have a net motion of the mean position of the walker. If , the walker on average moves steadily forward. If , the walker on average moves steadily backwards. The mean position of the walker is behaving as if it travels with a velocity,

where  is the time per step. This is different from the unbiased random walk with p=1/2 (or ), where the mean position stays fixed at the origin (check that for p=1/2, u=0).

However the walker is still diffusing about this mean position, with a root mean square average distance of . The diffusion constant D for this spread about the mean is given by,

yielding,

Such a biased random walk describes many physical processes in nature. For example, it describes the motion of a molecule of water in a pipe which has a steady flow of water with velocity u. When the water is flowing, the molecules are not all just moving uniformly down the pipe with constant speed u. Rather they are taking some complicated random path, colliding with each other and bouncing off each other in random directions, such that only on average are they drifting down the pipe with an average speed u. In between collisions, their speed  is generally very much larger than u -- this is because  is determined by the length and time scales of atomic collisions, whereas u is determined by , which is determined by the pressure difference causing the flow in the pipe. The molecules are taking a biased random walk. A similar biased random walk describes the motion of an electron in a current carrying wire.

Let's now consider a specific biased random walk: a gambler who bets only on "black" when playing at the roulette wheel. Since there are 38 numbers on the roulette wheel, of which only 18 are black (18 others are red, and then there are also the green "0" and "00"), the probability the gambler wins on any given spin is p = 18/38 = 9/19 = 0.474. If he makes $1 bets on each spin, the amount he has won (lost) after N spins is given by a biased random walk: with L = $1, the "distance" traveled is his net monetary balance; a positive distance is his net winnings in dollars, while a negative distance is his net loss in dollars.

After N spins of the wheel, his average expected loss (since p<1/2, on average he must always loses) in dollars is

How long does it take for his average loss to equal $1? i.e. for  = -1? It takes  spins. Even though on each bet he either wins $1 or loses $1, he will win almost as often as he loses, since p=9/19 is not too far from 1/2. It takes 19 spins before the slightly higher probability to lose results in a net average loss of $1. Similarly it takes  spins before his net average loss is equal to $M.

How big is the standard deviation about this loss?

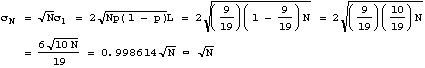
So in 19 spins, the average loss is $1, but the standard deviation about this loss is $ = $4.36. Therefore the likely range of winnings (with 95% confidence) after 19 spins is

-1 ± (2)(4.36) = -1 ± 8.72, or from -$9.72 to +$7.72

So even though the gambler on average loses $1 in 19 bets, in any one play of 19 bets, he still has a reasonable chance to come out ahead.

We can compute not only the mean and standard deviation of the amount won in N spins of the roulette wheel, but the entire probability distribution , the probability to have won $x in N spins of the wheel. To do this we note that if one has n wins in N spins of the wheel, then one also has N-n loses. The net winnings are therefore,

x = (+1)(n) + (-1)(N-n) = 2n-N

The probability to have n wins in N spins is just the binomial distribution,

So by knowing the probability to have n wins in N spins, and by knowing the winning x that corresponds to n wins, x=2n-N, we can combine these to get the probability to win $x in N spins, .

For example, we plot below the probability to have won $x after N spins of the wheel, for N=25, 100, and 400.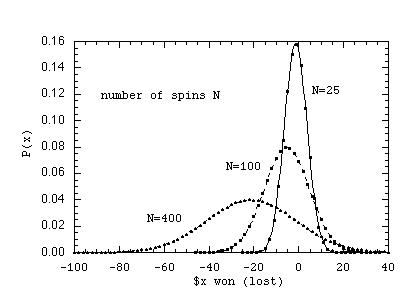 

One clearly sees that the probability distribution broadens, and shifts to the negative, as N increases. However we see that even after many spins, there remains a sizable probability to still come out a winner, with x>0.

We can be more quantitative about this as follows: The probability that the gambler comes out ahead, is the probability that his "distance traveled" in the random walk is greater than x=0. Since the mean distance after N steps is , the probability of a net winning is then equal to the probability that he is N/19 above the mean. How many standard deviations above the mean is this? Well the standard deviation for N steps is . So the number of standard deviations above the mean that we have to be in order to have a net winning is . What is the probability to be  standard deviations above the mean? Well, from the table in our text we can find the probability to be within the range  for various values of . If this probability is q, then there is a probability (1-q) to be either above  or below . But because the probability distribution is symmetric about the mean, half this (1-q) probability lies above , while half lies below . Hence the probability to lie above  is (1-q)/2. The number of spins associated with each value of  is given by , or . We can then make a table:

We can use this data to plot the probability of winning versus the number of spins of the roulette wheel.

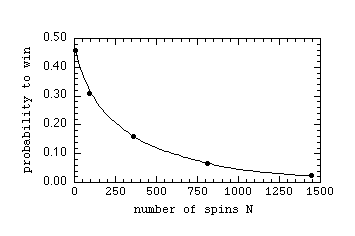
We see that the probability to win starts out at 9/19 = 0.474 on the first spin, and then steadily decreases. The probability to win will always be less than 1/2. This is how the casino stays in business!

Nevertheless, it is possible to devise a winning strategy to play roulette! With this strategy however, one can win, but not get rich! We do not have the mathematical tools to calculate the exact probabilities associated with this winning strategy, but we can get an intuitive feel for it as follows.

Consider which is more likely: In betting on black when playing roulette, making $1 bets each spin, is it more likely that one will first win $2 before losing $100? In terms of the biased random walk, is it more likely that our walker will first pass through the point +2 before he walks to a distance -100? By considering the probability distributions, we argue as follows that the answer is yes.

We have seen that the width of the probability distribution is growing like , while the mean is decreasing as -(1/19)N. In particular, after 25 spins, the width is 5, while the mean is -25/19 = -1.316. Since 5-1.316 = 3.684 is still more than one and a half times 2, we thus see that after 25 spins, there is still a fairly large probability to be at position +2 (or greater); however since the width 5 is very much smaller than 100, there is an extremely small probability that one is at position -100 (or less). Thus it is reasonable to expect that the walker has a much greater probability to pass first through the point +2 than he has to pass first through the point -100.

Our strategy for roulette is therefore as follows: Start with an initial stake of $100. Bet on black, and play until you either win $2 (at which point you quit) or lose all $100. By the above argument, we have a very much greater probability to win rather than lose. In fact, one could in principle calculate, given any size initial stake, how much to try to win before quitting, so as to have a probability to win arbitrarily close to unity. However the more you try to increase your odds of winning, the smaller is the amount you will win. Thus we have a strategy virtually guaranteed to win, but the amount you win will always be a rather small fraction of what you started with! You can't get rich with this strategy!

You might think to beat this catch-22 by the following thinking: Suppose you arrange it so that the probability to win with this strategy is p, with p very close to one, and so the amount that you win is therefore rather small. Why not try to increase your winnings just by playing this strategy over many times? Each time you will have a high probability to win, and so you just keep collecting your winnings until they add up to something substantial!

But for this to work, you have to win every single time you play the strategy! If you ever lose, you lose your entire stake and cannot continue! If you play the strategy N times, the probability to win all N times is . Since p is less than unity,  steadily decreases as N increases, while the probability to lose, , steadily increases. Clearly one cannot play too many times before losing gets too risky (for example, if p=0.95, then after 12 plays = 0.54, giving a 1-0.54 = 0.46 or 46% chance to lose). Thus there is no way around it - one can't get rich with this strategy.