We now consider a modification of the random walk. A random walker in the plane moves at each step with equal probability either upwards, downwards, to the left, or to the right. Imagine that we start the walker at some randomly chosen site on the boundary of a square. If he walks out of the square, we start over with a new walker at a new randomly chosen site. At the center of the square is a fixed "seed". If the walker ever reaches a site which borders on the seed, the walker sticks to the seed and remains there. We then start with a new walker randomly chosen again on the boundary of the square. He walks until he either walks out of the square, or else reaches a site which borders on the now larger seed in which case he sticks and remains there. In this way we grow an object in the center of the square. Such a process is known as "diffusion limited aggregation", and the object that grows is called a "DLA cluster."

After many such walkers stick on, what will be the shape of the growing seed? A natural guess is that, since walkers enter equally likely from all directions, one will grow a filled in circle, or perhaps a filled in square. Instead, one finds the following object shown below (this object is the result of 900 walkers sticking to the seed - the boundary in this example happened to be rectangular, not square, which is why the object is stretched more in the horizontal direction).

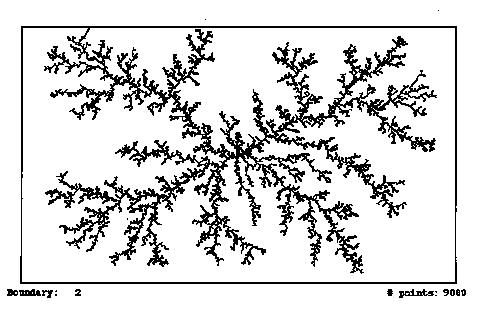
Such an object is called a fractal. A fractal is an object that looks the same on all length scales. For example, the fractal above consists of big branches which shoot off smaller branches, which shoot off still smaller branches, and so on. A fractal is also an object which can be thought of as having a non-integer dimension.

For example, suppose we measure length in units of "a" (you may think of "a" as being one inch, or one centimeter, or any other unit of length). Then in a line of length L, the number of such units that fill up the line is N = L/a ~L¹.

If we have a square with side of length L, and we measure area in units of a², then the number of such units that fill up the square is N = L²/a² ~ L².

If we have a cube with side L, and we measure volume in units of a³, then the number of such units that fill up the cube is N = L³/a³~L³.

In each case we found that the number of units that fill up the object is proportional to L^D where L is the characteristic length of the object, and D is the dimension. For the fractal above, the number of units N that make up the fractal (in the DLA cluster this is just the number of attached walkers) scales as N ~L^D, where D ~ 1.6 is a non-integer number. We can guess that for the DLA fractal  1 < D < 2 -- the fractal has greater extent than a line, as it spreads out in the plane, hence 1 < D; however it does not fill up any area uniformly - large holes are always left behind, so D < 2. D is called the fractal dimension.

Calculating the properties of a DLA cluster, such as its fractal dimension, or the rate of growth at various points on its various branches, is very much a topic of current research in theoretical physics. The DLA cluster is an example of how very complex behavior can arise from very simple and easily understood basic rules.