Problem Set 2

Problem Set 2

Due Tuesday, February 16, by 4pm in the homework locker

Problem 1 [10 points]
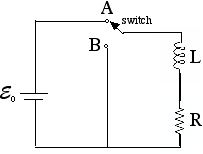
Suppose the circuit in the figure below has been connected for a long time to the battery (switch is in position A). Then at time t=0 the switch is thrown from position A to position B, cutting off the battery.
a) What is the current I(t) for all later times?
b) What is the total energy delivered to the resistor?
c) Show that this is equal to the energy originally stored in the inducotor.
Problem 2 [10 points]
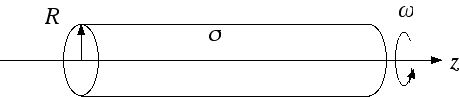
An infinite cylinder of radius R carries a uniform surface charge desnity σ. Suppose the cylinder is spun up about its axis starting from rest to a final angular velocity ω_f. How much work does this take, per unit length? Do the calculations two ways, as outlined below, and compare your answers. You should find that they are equal!
a) Find the magnetic field B and the induced electric field E (in the quasistatic approximation where one can compute B as in magnetostatics). Using this information, compute the net torque N, per unit length, on the cylinder, and then compute the work associated with rotating the cylinder against this torque, W = ∫ N dφ.
b) Compute the total energy stored in the magnetic field B in the final configuration.
Problem 3 [10 points]
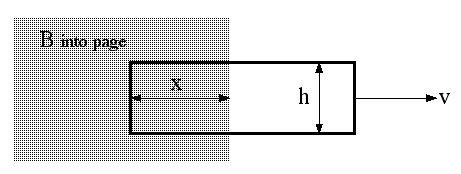
In the discussion of motional emf, as in Sec. 7.1.3 of Griffiths, it was assued tha the moving wire loop had a resistance R (see sketch below). The current in the loop generated by the loop's motion with speed v was then I = vBh/R. Suppose, however, that the wire is made of a perfectly conducting material, so that R is zero. In that case, the current is limited only by the back emf associated with the self inductance of the loop L (which ordinarily would by negligible in comparison with IR). Show that in this case the loop with total mass m oscillates with simple harmonic motion, and find its frequency of oscillation ω.
Problem 4 [10 points]
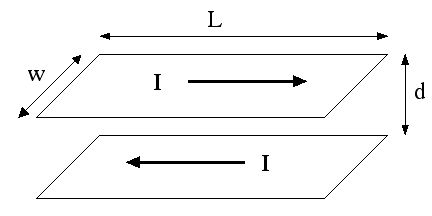
a) Consider two parallel planes of width w, and length L >> w, separated from each other by a distance d << w, as in the sketch below. A total current I, uniformly distributed over the surface of the upper plane, flows down the upper plane to the right. An equal current I, uniformly distributed over the surface of the lower plane, flows down the lower plane to the left. The upper plane is held at an electrostatic potential V with respect to the lower plane. Calculate the power (energy per unit time) transported down the length of the planes. In what direction is it flowing?

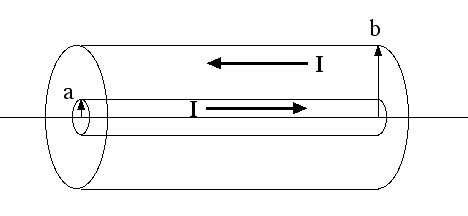
b) Consider a long coaxial cable as in the sketch below. A total current I, uniformly distributed over the surface of the inner cylinder of radius a, flows down the inner cylinder to the right. An equal total current I, uniformly distributed over the surface of the outer cylinder of radius b, flows down the outer cylinder to the left. The outer cylinder is held at an electrostatic potential V with respect to the inner cylinder. Calculate the power (energy per unit time) transported down the cable. In what direction is it flowing?
Problem 5 [10 points]
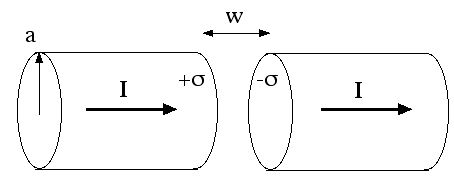
A fat wire of radius a, as in the sketch below, carries a constant current I, uniformly distributed over its cross section. A narrow gap in the wire of width w << a forms a parallel plate capacitor.
a) Find the electric and magnetic fields in the gap in the wire, as a function of the distance r from the axis of the wire, and time t. (assume the charge on the capacitor is zero at t=0)
b) Find the electromagnetic energy density u_EM and the Poynting vector S in the gap. Make sure to specify the direction of S. Check that your u_EM and S obey the equation of local energy conservation:
∂u_EM/∂t +∇·S = 0
c) Determine the total energy in the gap, as a function of time. Calculate the total power flowing into the gap, by integrating the flux of the Poynting vector through the appropriate surface. Check that the power flowing in is equal to the rate of increase of the energy in the gap.