Problem 1 [30 points]
Consider as a simplified model for the frequency dependent permittivity function
| ε(ω)/ε0 = 1 + | ωp2
ω02 − ω2 |
(This is the model discussed in lecture in the limit that the damping force vanishes.) Assume ω0 < ωp.
a) Using the dispersion relation k2 = (ω2/c2)(ε(ω)/ε0), make a sketch of k vs ω for electromagnetic wave propagation.
b) Re-draw this sketch as ω vs k, and show that for each value of k > 0 there are two allowed values (modes) of ω for the electromagnetic waves. Show that at both small k and at large k one of these two modes has a dispersion relation characteristic of an electromagnetic wave in the vacuum, i.e. ω = vpk where vp is only weakly dependent on k. Show that the other mode has a frequency ω that is, to lowest order, independent of k and so like some internal atomic mode of vibration. Show that these two modes exchange their characteristic behavior as one crosses from small k to large k. In this intermediate region the modes have a mixed character and are referred to as "polaritons".
c) Show that, for a given value of k, the higher frequency mode has a phase velocity that satisfies vp > c, while the lower frequency mode satisfies vp < c. Show that for both modes the group velocity always satisfies vg < c. You may demonstrate this either algebraically or graphically.
Problem 2 [20 points]
The longitudinal oscillations of the electric field in a conductor at frequency ω = ωp can be viewed physically in terms of the following simple model:
Consider a slab of conductor in which the charges consist of a fixed uniform background density of positive ionic charge, +eN, and an equal, but moveable, uniform density of negative electonic charge, −eN. When the negative charge density sits exactly on top of the positive charge density the system is neutral everywhere and the electric field inside the conductor is E = 0. Now displace the center of mass of the negative charge density by an amount δx, as shown in the sketch below.
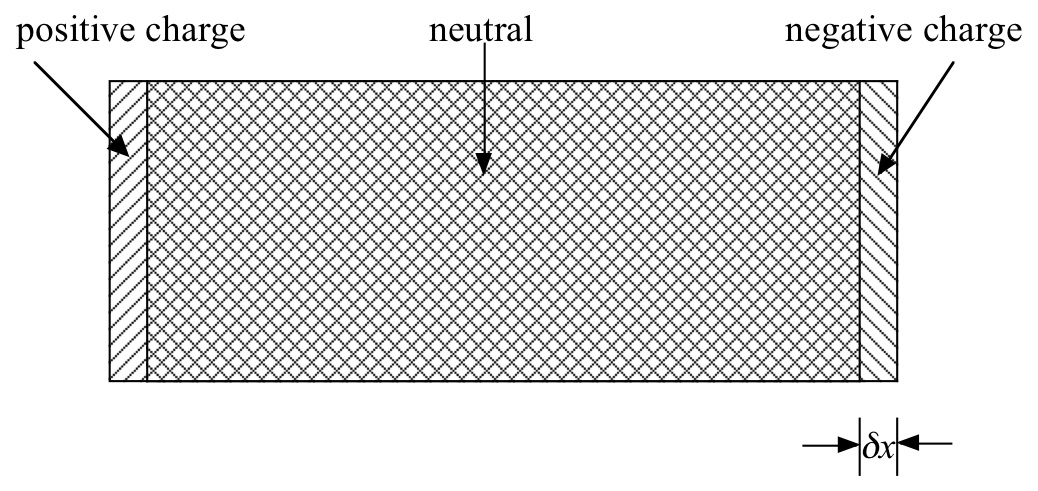
a) What surface charge density σ builds up on the ends of the conductor?
b) What is the E field created inside the conductor by this σ? (hint: it is just like a parallel plate capacitor) Express E as a function of δx and the density of electrons N.
c) Assuming that the electrons move together as a rigid body, what is the total force on the electrons due to the electric field E of part (b)? Write Newton's equation of motion for the center of mass of the electrons and show that the solution is an oscillation of δx with frequency ωp, where ωp is the plasma frequency discussed in lecture.
This oscillation in δx results in an oscillation in the uniform E of part (b), as well an an oscillation in the surface charge σ. This is called the plasma oscillation.