Problem 1 [15 points]
Consider a flat conducting sheet lying in the xy-plane at z=0. The sheet is electrically neutral (no net charge) and is carrying a steady uniform (magnetostatic) sheet current K = Kŷ in the y-direction. It may help conceptually to think of the sheet as having length L, width W, and small thickness d, as in the sketch below, with a uniform current denisty j=jŷ flowing through the cross-sectional area dW, so that K=jd. But we are interested in the limits that L and W get infinitely large, while d becomes infintestmally small.
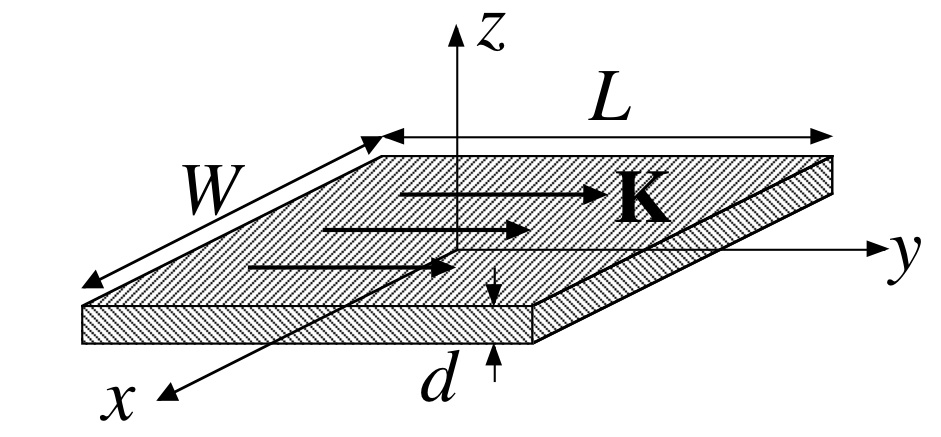
a) Find the electric and magnetic fields E and B for the above configuration.
b) Consider the above configuration as the inertial rest frame 𝒦 of the sheet. Consider now making a Lorentz transformation to an inertial frame 𝒦' that moves with velocity v=vŷ as seen by 𝒦. What are the electric and magnetic fields E' and B' that are seen in frame 𝒦'?
c) If you did part (b) correctly, you will find that E' ≠ 0. Show explicitly that this E' results from the presence of a charge density on the sheet, as seen in 𝒦'. Explicitly find this charge density by making a Lorentz transformation of the 4-current from 𝒦 to 𝒦'.
d) Where does this charge come from, given that the sheet is neutral in frame 𝒦? Give a physical answer in terms of simple concepts from relativity, like time dilation or FitzGerald contraction (rather than from the machinery of 4-vectors and trasformation matrices). You only have to give a good explanation, you do not need to do a calculation.
e) Is there a frame 𝒦' in which B' = 0? Explain your answer.
Problem 2 [10 points]
Show that the ordinary acceleration a=dv/dt of a particle of mass m and charge q, moving at velocity v under the influence of electromagnetic fields E and B, is given by,
a = (q/m) (1 - v2/c2)1/2 [ E + v×B - v ( v·E)/c2 ]
Remember to use the correct relativistic form for momentum, p = mγv, in Newton's equation F = ma.