- Problem 1 [10 points]
In lecture, when we derived the following expression for the energy stored in a configuration of magnetostatic currents,
Wmag = (1/2)∫ d3r j(r)⋅A(r)
we assumed that the vector potential A was in the Coulomb gauge, i.e. that ∇⋅A = 0.
Show that in fact this expression is correct even when A is not in the Coulomb gauge.
Hint: Suppose A is in the Coulomb gauge. Construct another vector potential by taking A'(r) ≡ A(r) + ∇χ(r), where χ(r) is any scalar function. Note, this A'(r) is a good vector potential, i.e. it gives the same B = ∇×A' as does A, however A' does not in general satisfy ∇⋅A' = 0. Show that Wmag = ∫ d3r j(r)⋅A'(r) still gives the correct energy stored in the configuration.
- Problem 2 [10 points]
Use the formalism of the Levi-Civita tensor εijk to derive the following vector identities:
a) ∇×(fg) = f(∇×g) − g×(∇f) where f is any scalar function and g is any vector function
b) ∇×(∇×A) = −∇2A +∇(∇⋅A)
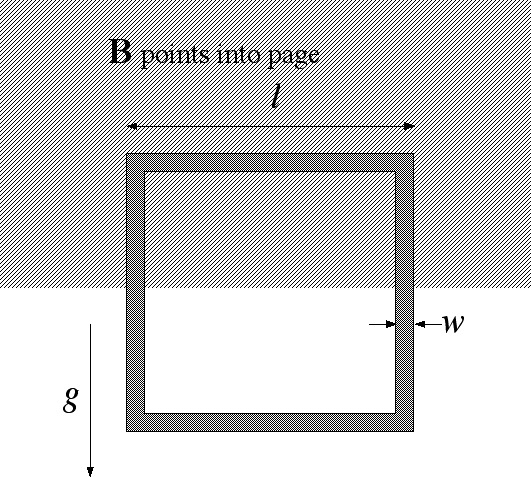
- Problem 3 [10 points]
A square ring of length ℓ and width w is cut out of a thick sheet of aluminum. It is then placed so that the top portion of the ring is in a uniform magnetic field B. At time t=0 the ring, initially at rest, is let go and falls under the influence of gravitational acceleration g, as in the diagram below. What is the terminal velocity of the ring (i.e. the velocity at long times, though assume that the upper segment of the ring is always within the magnetic field) as a function of the magnitude of the magnetic field B, the resistance of the ring R, and the total mass of the ring m? Find the velocity of the ring as a function of time. What would happen if you cut a tiny slit in the ring, breaking the circuit?
- Problem 4 [10 points]
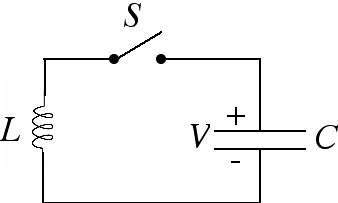
A capacitor C is charged up to a voltage V and connected to an inductor L, as shown in the diagram below. At time t = 0, the switch S is closed. Find the current in the circuit as a function of time. How does your answer change if a resistor R is included in the circuit in series with C and L? (Hint: recall that the capacitance is defined by C = Q/V, where Q is the total charge on one of the plates, and V is the voltage drop across the plates. The current flowing in a circuit is just I = dQ/dt.)
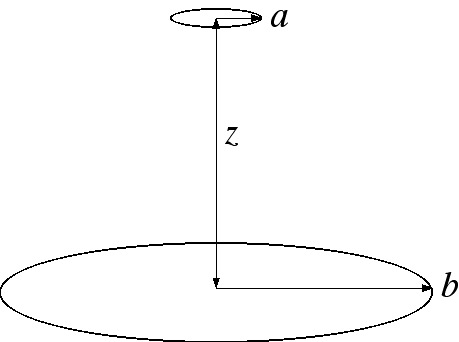
- Problem 5 [10 points]
A small loop of wire with radius a is held a distance z above the center of a large loop of wire of radius b, as shown in the figure below. The planes of the two loops are parallel and perpendiculat ro the common axis.
(a) Suppose current I flows in the big loop. Find the magnetic flux through the little loop (you may assume that the little loop is so small that you may approximate the field of the big loop to be constant over the area of the small loop).
(b) Suppose current I flows in the little loop. Find the magnetic flux through the big loop (you may assume the little loop is so small that you may treat it as a point magnetic dipole).
(c) From the results of the previous parts, find the mutual inductances of the two loops and confirm that M12 = M21
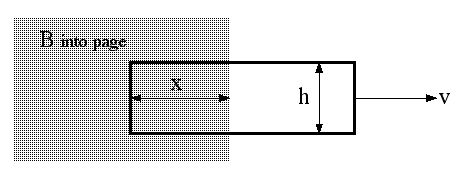
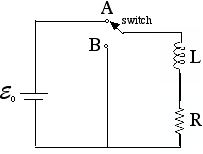
- Problem 6 [10 points]
Suppose the circuit in the figure below has been connected for a long time to the battery (switch is in position A). Then at time t=0 the switch is thrown from position A to position B, cutting off the battery.
a) What is the current I(t) for all later times?
b) What is the total energy delivered to the resistor?
c) Show that this is equal to the energy originally stored in the inducotor.
- Problem 7 [10 points]
In the discussion of motional emf, as in Sec. 7.1.3 of Griffiths, it was assued tha the moving wire loop had a resistance R (see sketch below). The current in the loop generated by the loop's motion with speed v was then I = vBh/R. Suppose, however, that the wire is made of a perfectly conducting material, so that R is zero. In that case, the current is limited only by the back emf associated with the self inductance of the loop L (which ordinarily would by negligible in comparison with IR). Show that in this case the loop with total mass m oscillates with simple harmonic motion, and find its frequency of oscillation ω.