Problem Set 3

Problem Set 3

Due Friday, February 17, by 4pm in the homework locker

Problem 1 [10 points]
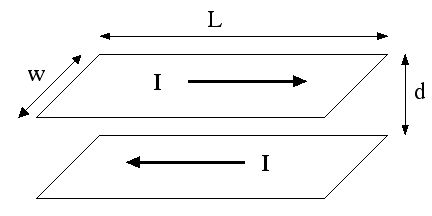
a) Consider two parallel planes of width w, and length L >> w, separated from each other by a distance d << w, as in the sketch below. A total current I, uniformly distributed over the surface of the upper plane, flows down the upper plane to the right. An equal current I, uniformly distributed over the surface of the lower plane, flows down the lower plane to the left. The upper plane is held at an electrostatic potential V with respect to the lower plane. Calculate the power (energy per unit time) transported down the length of the planes. In what direction is it flowing?

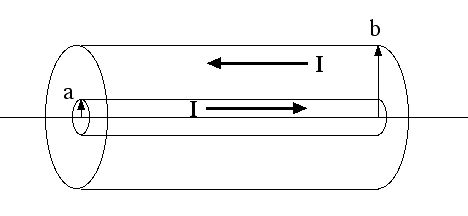
b) Consider a long coaxial cable as in the sketch below. A total current I, uniformly distributed over the surface of the inner cylinder of radius a, flows down the inner cylinder to the right. An equal total current I, uniformly distributed over the surface of the outer cylinder of radius b, flows down the outer cylinder to the left. The outer cylinder is held at an electrostatic potential V with respect to the inner cylinder. Calculate the power (energy per unit time) transported down the cable. In what direction is it flowing?
Problem 2 [10 points]
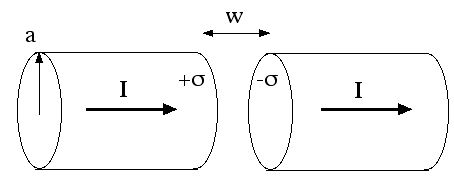
A fat wire of radius a, as in the sketch below, carries a constant current I, uniformly distributed over its cross section. A narrow gap in the wire of width w << a forms a parallel plate capacitor.
a) Find the electric and magnetic fields in the gap in the wire, as a function of the distance r from the axis of the wire, and time t. (assume the charge on the capacitor is zero at t=0)
b) Find the electromagnetic energy density u_EM and the Poynting vector S in the gap. Make sure to specify the direction of S. Check that your u_EM and S obey the equation of local energy conservation:
∂u_EM/∂t +∇·S = 0
c) Determine the total energy in the gap, as a function of time. Calculate the total power flowing into the gap, by integrating the flux of the Poynting vector through the appropriate surface. Check that the power flowing in is equal to the rate of increase of the energy in the gap.
Problem 3 [10 points]
a) Consider two equal point charges q, separated by a distance 2a. Consider the plane that is equidistant from the two charges. By integrating Maxwell's stress tensor over this plane, determine the force of one charge on the other, and show that it agrees with what you would expect.
b) Do the same for two charges that are opposite in sign.
Problem 4 [20 points]
Imagine the electon as a classical sphere of radius R, that has a uniform surface charge density with total charge -e, and is spinning about the z axis with angular velocity ω.
(a) Calculate the total energy contained in the electromagnetic fields (you of course have to first find, or look up, the E and B fields for this configuration).
(b) Calculate the total angular momentum contained in the electromagnetic fields.
(c) According to Einstein's formular E=mc², the energy contained in the electromagnetic fields should contribute to the mass of the electron. Suppose that all the rest mass of the electron is made of this electromagnetic energy. Similarly, imagine that the intrinsic angular momentum of the electron, hbar/2, is given by the total angular momentum of the electromagnetic fields. What would the radius R of the electron and its angular velocity ω have to be in order to get the observed electron rest mass and intrinsic angular momentum? Do these answers make physical sense?
Problem 5 [10 points]
(a) Find the electric and magnetic fields, and the charge and current densities, corresponding to the potentials

V(r,t)=0 and A(r,t) = -1
4πε₀ qt
r² r̂

(b) Use the gauge function λ(r,t) = -(1/4πε₀)(qt/r) to transform the potentials, and comment on the result.