| |

Home
Contact Info
Course Info
Calendar
Homework
Lecture Notes
|
|
|
|
PHY 218: Electricity and Magnetism II
Prof. S. Teitel stte@pas.rochester.edu ---- Spring 2017
Problem Set 6
Due Friday, March 31, by 4pm in the homework locker
- Problem 1 [15 points]
The longitudinal oscillations of the electric field in a conductor at frequency ω = ωp can be viewed physically in terms of the following simple model:
Consider a slab of conductor in which the charges consist of a fixed uniform background density of positive ionic charge, +eN, and an equal, but moveable, uniform density of negative electonic charge, −eN. When the negative charge density sits exactly on top of the positive charge density the system is neutral everywhere and the electric field inside the conductor is E = 0. Now displace the center of mass of the negative charge density by an amount δx, as shown in the sketch below.
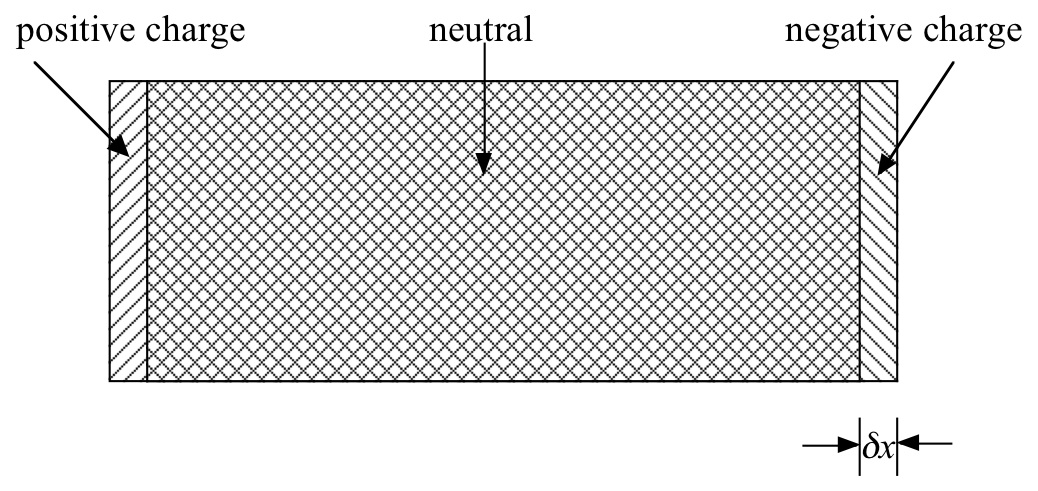
a) What surface charge density σ builds up on the ends of the conductor?
b) What is the E field created inside the conductor by this σ? (hint: it is just like a parallel plate capacitor) Express E as a function of δx and the density of electrons N.
c) Assuming that the electrons move together as a rigid body, what is the total force on the electrons due to the electric field E of part (b)? Write Newton's equation of motion for the center of mass of the electrons and show that the solution is an oscillation of δx with frequency ωp, where ωp is the plasma frequency discussed in lecture.
This oscillation in δx results in an oscillation in the uniform E of part (b), as well an an oscillation in the surface charge σ. This is called the plasma oscillation.
- Problem 2 [15 points]
Using our results from lecture for the reflection coefficients:
| R⊥ = | |
μbkIz−μakTz
μbkIz+μakTz | |2, |
|
R|| = | |
εbkIz−εakTz
εbkIz+εakTz |
|2 |
and the transmitted amplitudes
| ET⊥ = |
2μbkIz
μbkIz+μakTz |
EI⊥, |
|
HT|| = |
2εbkIz
εbkIz+εakTz |
HI|| |
and defining the transmission coefficients by
where <S> = (1/μ)<E×B> = <E×H> is the time averaged Poynting vector in the corresponding material, and n is the unit normal to the interface, show explicitly that
T⊥ + R⊥ = 1 and T|| + R|| = 1.
- Problem 3 [20 points]
Find the transmission coefficient for a transverse polarized plane electromagnetic wave of frequency ω passing through a plate of glass of thickness d, where the wave hits the glass at normal incidence, i.e. θI = 0. Take the air on either side of the glass to have an index of refraction equal to unity, while the index of refraction of the glass is n. Assume the magnetic permeability in all regions is just μ0.
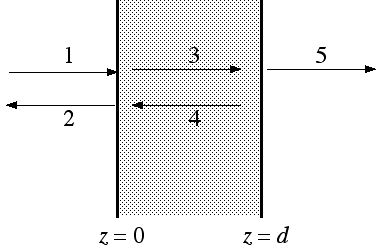
Keep in mind that at each of the two interfaces there is both a reflected and transmitted wave, as in the sketch below, and that the boundary condition on the electric field applies to the total electric field on each side of the interface.
Using the boundary condition on electric field, write the complex amplitude Ei for each of the components in the sketch in terms of the incident amplitude E1, and then find the transmission coefficient by T = |E5|2/|E1|2.
|
|