Problem 1 [30 points]
Consider a classical model of the Helium atom as shown below. Two electrons, each with charge -e, orbit together on opposite sides of a nucleus of charge +2e. The radius of the orbit is a0, and the electrons orbit with a speed v, giving an angular velocity of ω0 = v/a0. The goal of this problem is to compute the radiation that would be emitted in this classical model.
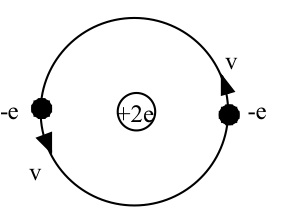
a) Show that there is no electric dipole radiation in this model.
b) Show that there is no magnetic dipole radiation in this model.
c) Compute the electric quadrapole tensor and show that it does not vanish. What is its frequency of oscillation?
d) Find Qω, the tensor that gives the amplitude of the electric quadrapole oscillation, i.e. Q(t) = Re [ Qω e-iωt]. Then using the solution to problem 2 on last week's Problem Set 7, find the amplitudes Eω(r) and Bω(r) of the oscillations of the radiated electric and magnetic fields (in the Radiation Zone limit).
e) Find the angular distribution dP/dΩ of the radiated power, and sketch a polar plot of your result.
(Note: the electric quadrapole tensor you find in this problem will not be the same form as in part (d) of Problem Set 7, problem 2; in that case we assumed Qω was real, while here you should find that it is complex. Hence the angular distribution of the radiation will not be the same as was found there.)
Problem 2 [15 points]
Using the expressions found in lecture for the electric and magnetic fields of a charge moving with a small uniform velocity v (v << c), compute the total momentum PEM carried by the electromagnetic fields of the charge. Recall, PEM = ∫d3r pEM, where the electromagnetic momentum density is pEM = ε0μ0S = ε0E×B.
Show that to lowest order in v, PEM = (4/3) (U/c2)v, where U is the total electromagnetic energy stored in the fields of the charge.
(Hint: the algebra only works nicely if you do the calculation to lowest order in v.)