Problem Set 2

Problem Set 2

Due Wednesday, November 8, in lecture

Problem 1 [20 points]
The Bohr-Sommerfeld quantization condition (a precursor to modern quantum mechanics) claimed that a particle could be in a periodic orbit only if the circumference of the orbit contained an integral number of de Broglie wavelengths.
Consider a classical particle moving in a uniform magnetic field H in the z direction. Use the Bohr-Sommerfeld quantization condition to determine the allowed orbital radii, and energies of this motion. Compare these energies to the energies of the Landau levels (i.e. the exact eigenvalues of the Schrodinger equation). Show that each successive orbit encloses exactly one additional quantum of flux φ₀ of magnetic field.
Hint: It is important to remember that the de Broglie wavelength is determined by the canonical momentum p, and that p is related the the mechanical momentum mv by p = mv - (e/c)A, where A is the vector potential. This calculation is simplified if one uses the symmetric gauge A=−(1/2)r×H, in which the vector potential is purely azimuthal and independent of the azimuthal angle.
Problem 2 [20 points]
Consider the rectangular geometry used in lecture: system length L, width W, periodic boundary conditions along x, y restricted to interval [0,W], uniform magnetic field H along z, and uniform electric field E in the y direction. Show by an explicit quantum mechanical calculation of the currents that for a filled Landau level,
ρ_xx = 0, and ρ_xy = h/e²
The currents for Landau level n are given by,

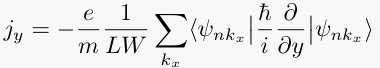
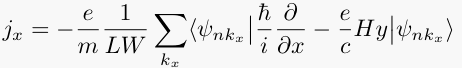
where the gauge A_x = Hy, A_y = 0, has been used for the vector potential, and where the eigen-wavefunctions are

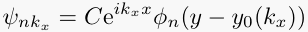
where C is a normalization constant,

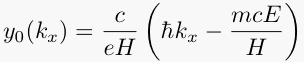
and φ_n is the wavefunction for the nth excited state of the harmonic oscillator.
Problem 3 [15 points]
a) For the Integer Quantum Hall Effect, why was it necessary that the electron gas be considered two dimensional?
b) The Integer Quantum Hall Effect was first observed in semiconductor inversion layers. Explain why you could probably not see the Integer Quantum Hall Effect in a thin monolayer metallic film. Your argument should involve some relevent numerical estimates such as the density of conduction electrons in a typical metal, and the strength of a typical large laboratory magnetic field (~ 10 tesla).
Caution: To do part (b) you will need to use the numerical value of the flux quantum φ₀. In CGS units (as used in lecture), φ₀=hc/e and has the units of statvolt-cm. In MKS units, φ₀=h/e and has the units of volt-cm. If you need to refresh yourself on CGS vs MKS units in electromagnetism, see Classical Electrodynamics, by Jackson, Appendix A.
Problem 4 [10 points]
Consider a point charge Q placed in a free electron gas with screening length 1/k₀. By considering the induced charge created by Q, compute the total charge Q(r) contained within a sphere of radius r centered on the point charge. Sketch how Q(r) varies with distance r.