Home

Contact
Info

Course
Info

Calendar

Homework

Lecture
Notes

Physics 415: Electromagnetic Theory I
Prof. S. Teitel stte@pas.rochester.edu ----- Fall 2002

Problem Set 2

Due Wednesday, October 2, in lecture

• Problem 1 [10 points]

  a) In lecture we solved the problem of the electric field from a spherical shell of radius R with uniform surface charge = q/4R². Consider now the problem where this shell is smeared out over a thickness d. That is, there is a uniform charge density per volume in a spherical shell of finite thickness from radius R to radius R+d. Find the potential (r) by solving Poisson's equation (there may be easier ways to do it, but do it this way), then take the gradient to get E(r). Sketch (r) and E(r) vs. r. Now take the limit d->0, keeping d = constant. Compare your result with the case of the infinitesmally thich shell done in lecture.

  b) Consider an infinitesmally thin spherical shell of radius R with total charge q, and a concentric infinitesmally thin spherical shell of radius R+d with total charge -q. Find the potential (r) by directly solving Poisson's equation for this geometry, then take the gradient to get E(r). Sketch (r) and E(r) vs. r. Now take the limit d->0, keeping qd constant. What do you find? This is the limit of an infinitesmally thin dipole layer.

• Problem 2 - Jackson problem 1.12 [10 points]

  Prove Green's reciprocation theorem: If is the potential due to a volume charge density within a volume V and a surface charge density on the conducting surface S bounding the volume V, while ´ is the potential for the same geometry but for a different ´ and ´, then

  _V d³r ´ +_S da ´ = _V d³r ´ +_S da ´

• Problem 3 - Jackson problem 1.13 [10 points]

  Two infinite grounded parallel conducting planes are separated by a distance d. A point charge q is placed between the planes. Use the reciprocation theorem of Green to prove that the total induced charge on one of the planes is equal to (-q) times the fractional perpendicular distance of the point charge from the other plane. (Hint: As your comparison electrostatic problem with the same surfaces choose one whose charge densities and potential are known and simple.)

• Problem 4 [10 points]

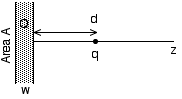
  Consider a point charge q a distance d in front of a plane conducting slab of thickness w, as shown below. The slab has a fixed net charge Q on it. Find the electric field on both sides of the slab. Find the force between the charge q and the slab. For this problem, assume that the side area of the slab A is finite, so that the average surface charge Q/2A is finite; however you make work the problem out ignoring edge effects, i.e. assuming the plane is effectively infinite.

  

• Problem 5 - Jackson problem 2.2 [10 points]

  Using the method of images, dicuss the problem of a point charge q inside a hollow, grounded, conducting sphere of inner radius a. Find

  a) the potential inside the sphere;
  b) the induced surface charge density; what is the total induced charge?
  c) the magnitude and direction of the force acting on q. Does q get pushed towards the center, or away from the center?
  d) Is there any change in the solution if the sphere is kept at a fixed potential _o? If the sphere has a fixed total charge Q?