Home

Contact
Info

Course
Info

Calendar

Homework

Lecture
Notes

Physics 415: Electromagnetic Theory I
Prof. S. Teitel stte@pas.rochester.edu ----- Fall 2003

Problem Set 6

Due Wednesday, December 3, in lecture

• Problem 1 [10 points]

  Consider a parallel plate capacitor of surface area A and separation d. A free charge Q is added to the upper plate, and a free charge -Q is added to the lower plate. If the resulting potential drop between the two plates is V, find the capacitance C=Q/V, when the space between the two plates is half filled with a dielectric material of dielectric constant . Find C for both of the two geometries shown below. You may ignore edge effects.

  

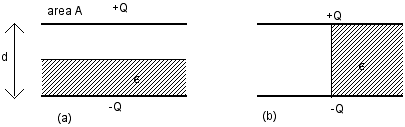
• Problem 2 [10 points]

  Consider a parallel plate capacitor of surface area A, separation d, and length w. A free charge Q is on the upper plate, and a free charge -Q is on the lower plate. A dielectric material of dielectric constant is inserted a distance x into the space between the plates.

  a) Compute the electrostatic energy stored in the configuration (you can either use the capacitance, similar to what you computed in problem 1b, or, to avoid double jepordy, try to do it another way!).

  b) Use the method of virtual work to compute the force on the dielectric. Be sure to give the direction of the force.

     

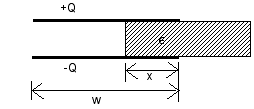
• Problem 3 [10 points]

  Consider a spherical conducting shell of radius R, with a total charge Q. Compute the total force on the northern hemisphere.

• Problem 4 [10 points]

  Two infinite parallel wires carrying currents I₁ and I₂ are separated by a distance d. Compute the flux of electromagnetic momentum, -da T·n, passing through an infinite plane half way between the two wires; the normal n to the plane is in direction d. Consider both the cases where the currents are parallel and anti-parallel. Interpret your answer.

  

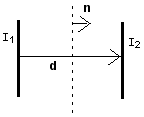
• Problem 5 [10 points]

  Consider a set of charged particles contained in the volume V, bounded by the surface S. Show that the angular momentum conservation law for the combined system of particles and electromagnetic field can be expressed as

  

  where L^mech is the total mechanical angular momentum of the moving charges, the angular momentum density of the electromagnetic field is

  

  and the tensor M is related to the Maxwell stress tensor by

  M_ij = _{i k m} r_k T_mj

  where _{i k m} is the Levi-Civita tensor.