|
|

Home
Contact
Info
Course
Info
Calendar
Homework
Lecture
Notes
|
|
|
|
Physics 415: Electromagnetic Theory I
Prof. S. Teitel stte@pas.rochester.edu ----- Fall 2004
Problem Set 6
Due Wednesday, November 24, in lecture
- Problem 1 [10 points]
Consider two equal point charges q separated by a distance r. Consider the plane that is equidistant from the two charges. By integrating the Maxwell stress tensor over this plane, determine the force of one charge on the other. Do the same for charges of opposite sign.
- Problem 2 [15 points]
Consider, as a classical model of an electron, a uniformly charged spherical shell
with charge e and radius R, spinning with angular velocity  . .
a) Compute the total energy contained in the electromagnetic fields.
b) Compute the total angular momentum contained in the electromagnetic fields.
If 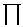 is the electromagnetic momentum density, then r is the electromagnetic momentum density, then r 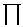 is the angular momentum density. is the angular momentum density.
c) According to Einstein, the rest energy of a particle is related to its rest mass by E=mc2. If one assumes that all the rest mass m is due to the energy
of the electron's electromagnetic field computed in (a), compute the radius R of the electron.
d) Assuming that the total angular momentum computed in (b) is equal to the intrinsic angular momentum of the electron, 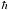 /2, compute the angular velocity /2, compute the angular velocity
 of the electron. of the electron.
e) Are your results in (c) and (d) physically reasonable for the electron?
- Problem 3 [15 points]
Consider as a very simplified model for the dielectric function,

(this is the model discussed in lecture in the limit that the damping force vanishes).
Assume  o < o <  p. p.
a) Using the dispersion relation k2 =  2 2 ( ( )/c2, make a sketch of k versus )/c2, make a sketch of k versus
 for electromagnetic wave propagation. for electromagnetic wave propagation.
b) Re-draw this sketch as  versus k, and show that for each value of k>0, there are two allowed values (modes) of versus k, and show that for each value of k>0, there are two allowed values (modes) of  for the electromagnetic waves.
Show that at both small k and at large k one of these two modes has a dispersion relation characteristic of an electromagnetic wave in the vacuum, ie. for the electromagnetic waves.
Show that at both small k and at large k one of these two modes has a dispersion relation characteristic of an electromagnetic wave in the vacuum, ie.  = vpk, where vp is only weakly dependent on k. Show that the other mode has a frequency = vpk, where vp is only weakly dependent on k. Show that the other mode has a frequency  that is, to lowest order, independent of k, and so like some internal atomic mode of vibration. Show that these two modes exchange their characteristic behavior, as one crosses from small to large k. In this intermediate region, the modes have a mixed character and are referred to as "polaritons." that is, to lowest order, independent of k, and so like some internal atomic mode of vibration. Show that these two modes exchange their characteristic behavior, as one crosses from small to large k. In this intermediate region, the modes have a mixed character and are referred to as "polaritons."
c) Show that for the higher frequency mode the phase velocity satisfies, vp>c, while for the lower frequency mode, vp<c. Show that for both modes, the group velocity always satisfies vg<c.
|

