| |

Home
Contact Info
Course Info
Calendar
Homework
Lecture Notes
|
|
|
|
PHY 415: Electromagnetic Theory I
Prof. S. Teitel stte@pas.rochester.edu ---- Fall 2008
Problem Set 5
Due Wednesday, November 12, in lecture
- Problem 1 [20 points]
A spherical dielectric shell, with inner radius a, outer radius b, and dielectric constant ε, is placed in a uniform external electric field Eo. Find the electric field outside the shell (r>b), inside the shell (r<a), and in the dielectric (a<r<b). What is the field inside the shell in the limit that ε gets infinitely large?
- Problem 2 [20 points]
An infinitely long cylindrical shell of inner radius a and outer radius b, and of magnetic permeability µ, is placed in a uniform extermal magnetic flux density Bo which is directed at right angles to the axis of the cylinder. Find the magnetic flux density B outside the cylinder (r>b), inside the cylinder (r<a), and within the shell (a<r<b). [Hint: express the magnetic field H in terms of a scalar potential, and use separation of variables in cylindrical coordinates.]
- Problem 3 [10 points]
Consider two equal point charges q separated by a distance r. Consider the plane that is equidistant from the two charges, i.e. the plane that bisects the vector r and has a normal vector parallel to r. By integrating the Maxwell stress tensor over this plane, determine the force of one charge on the other. Do the same for charges of opposite sign.
- Problem 4 [10 points]
Consider a spherical conducting shell of radius R that has a total charge Q. Compute the total force on the northern hemisphere of the shell.
- Problem 5 [15 points]
Consider, as a classical model of an electron, a uniformly charged spherical shell
with charge e and radius R, spinning with angular velocity ω.
a) Compute the total energy contained in the electromagnetic fields.
b) Compute the total angular momentum contained in the electromagnetic fields.
If Π is the electromagnetic momentum density, then r×Π is the angular momentum density.
c) According to Einstein, the rest energy of a particle is related to its rest mass by E=mc2. If one assumes that all the rest mass m is due to the energy
of the electron's electromagnetic field computed in (a), compute the radius R of the electron.
d) Assuming that the total angular momentum computed in (b) is equal to the intrinsic angular momentum of the electron, 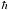 /2, compute the angular velocity
ω of the electron. /2, compute the angular velocity
ω of the electron.
e) Are your results in (c) and (d) physically reasonable for the electron?
|
|