| |

Home
Contact Info
Course Info
Calendar
Homework
Lecture Notes
|
|
|
|
PHY 415: Electromagnetic Theory I
Prof. S. Teitel stte@pas.rochester.edu ---- Fall 2010
Problem Set 6
Due Wednesday, November 24, in my mailbox
- Problem 1 [10 points]
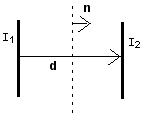
Two infinite parallel wires carrying currents I1 and I2 are separated by a distance d. Compute the flux of electromagnetic momentum -∫daT⋅n passing through an infinite plane half way between the wires; the normal n to the plane is in the direction d. Consider both the cases where the currents are parallel and anti-parallel. Interpret your answer.
- Problem 2 [10 points]
Consider a spherical conducting shell of radius R that has a total charge Q. Compute the total force on the northern hemisphere of the shell.
- Problem 3 [15 points]
Consider, as a classical model of an electron, a uniformly charged spherical shell
with charge e and radius R, spinning with angular velocity ω.
a) Compute the total energy contained in the electromagnetic fields.
b) Compute the total angular momentum contained in the electromagnetic fields.
If Π is the electromagnetic momentum density, then r×Π is the angular momentum density.
c) According to Einstein, the rest energy of a particle is related to its rest mass by E=mc2. If one assumes that all the rest mass m is due to the energy
of the electron's electromagnetic field computed in (a), compute the radius R of the electron.
d) Assuming that the total angular momentum computed in (b) is equal to the intrinsic angular momentum of the electron, 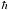 /2, compute the angular velocity
ω of the electron. /2, compute the angular velocity
ω of the electron.
e) Are your results in (c) and (d) physically reasonable for the electron?
- Problem 4 [15 points]
Consider as a very simplified model for the dielectric function
(This is the model discussed in lecture in the limit that the damping force vanishes.) Assume ω0 < ωp.
a) Using the dispersion relation k2 = ω2ε(ω)/c2, make a sketch of k vs ω for electromagnetic wave propagation.
b) Re-draw this sketch as ω vs k, and show that for each value of k > 0 there are two allowed values (modes) of ω for the electromagnetic waves. Show that at both small k and at large k one of these two modes has a dispersion relation characteristic of an electromagnetic wave in the vacuum, i.e. ω = vpk where vp is only weakly dependent on k. Show that the other mode has a frequency ω that is, to lowest order, independent of k and so like some internal atomic mode of vibration. Show that these two modes exchange their characteristic behavior as one crosses from small k to large k. In this intermediate region the modes have a mixed character and are referred to as "polaritons".
c) Show that, at a given value of k, the higher frequency mode has a phase velocity that satisfies vp > c, while the lower frequency mode satisfies vp < c. Show that for both modes the group velocity always satisfies vg < c.
|
|