| |

Home
Contact Info
Course Info
Calendar
Homework
Lecture Notes
|
|
|
|
PHY 415: Electromagnetic Theory I
Prof. S. Teitel stte@pas.rochester.edu ---- Fall 2011
Problem Set 5
Due Wednesday, November 16, in lecture
- Problem 1 [20 points]
A spherical dielectric shell, with inner radius a, outer radius b, and dielectric constant ε, is placed in a uniform external electric field Eo. Find the electric field outside the shell (r>b), inside the shell (r<a), and in the dielectric (a<r<b). What is the field inside the shell in the limit that ε gets infinitely large?
- Problem 2 [20 points]
An infinitely long cylindrical shell of inner radius a and outer radius b, and of magnetic permeability µ, is placed in a uniform extermal magnetic flux density Bo which is directed at right angles to the axis of the cylinder. Find the magnetic flux density B outside the cylinder (r>b), inside the cylinder (r<a), and within the shell (a<r<b). [Hint: express the magnetic field H in terms of a scalar potential, and use separation of variables in cylindrical coordinates.]
- Problem 3 [10 points]
Two infinite parallel wires carrying currents I1 and I2 are separated by a distance d. Compute the flux of electromagnetic momentum -∫daT⋅n passing through an infinite plane half way between the wires; the normal n to the plane is in the direction d. Consider both the cases where the currents are parallel and anti-parallel. Interpret your answer.
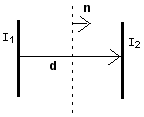
- Problem 4 [10 points]
Consider a spherical conducting shell of radius R that has a total charge Q. Compute the total force on the northern hemisphere of the shell.
|
|