Problem 3 [20 points]
Consider, as a classical model of an electron, a uniformly charged spherical shell
with charge e and radius R, spinning with angular velocity ω.
a) Compute the total energy contained in the electromagnetic fields.
b) Compute the total angular momentum contained in the electromagnetic fields.
If Π is the electromagnetic momentum density, then r×Π is the angular momentum density.
c) According to Einstein, the rest energy of a particle is related to its rest mass by E=mc2. If one assumes that all the rest mass m is due to the energy
of the electron's electromagnetic field computed in (a), compute the radius R of the electron.
d) Assuming that the total angular momentum computed in (b) is equal to the intrinsic angular momentum of the electron, 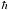 /2, compute the angular velocity
ω of the electron.
/2, compute the angular velocity
ω of the electron.
e) Are your results in (c) and (d) physically reasonable for the electron?