|
|

Home
Contact
Info
Course
Info
Calendar
Homework
Lecture
Notes
|
|
|
|
Physics 418: Statistical Mechanics I
Prof. S. Teitel stte@pas.rochester.edu ----- Spring 2004
Problem Set 6
Due Tuesday, April 27, in lecture
- Problem 1 [30 points total]
Consider an ideal Bose gas in three dimensions. In lecture
we considered how the specific heat at constant volume,
CV behaved as one approached the BEC transition temperature. Here we will investigate how the specific heat at constant pressure, Cp, behaves. This problem is Pathria problem 7.4. Note that CV = T(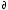 S/ S/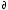 T)V,N, and
Cp = T( T)V,N, and
Cp = T(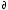 S/ S/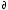 T)p,N, i.e. both are derivates taken keeping the number of particles N constant (i.e. not keeping fugacity z constant!). T)p,N, i.e. both are derivates taken keeping the number of particles N constant (i.e. not keeping fugacity z constant!).
a) Start by showing that for an ideal Bose gas,
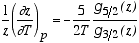
where z is the fugacity, and gx is the "standard" function defined in connection with Bose gases (Pathria Appendix D).
Hint: look back in the lecture notes at how we computed the corresponding derivative at constant density n=N / V, i.e. (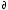 z/ z/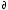 T)v (where v=1/n is the specific volume), in our calcuation of CV, and apply a similar trick to this case. [10 pts] T)v (where v=1/n is the specific volume), in our calcuation of CV, and apply a similar trick to this case. [10 pts]
b) Next compute the total entropy by using S = -(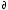 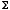 / /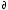 T)N,µ.
Then, compute the entropy per particle S/N, and show that you get Pathria Eq.(7.1.44a). You only have to do the case T>Tc. [10 pts] T)N,µ.
Then, compute the entropy per particle S/N, and show that you get Pathria Eq.(7.1.44a). You only have to do the case T>Tc. [10 pts]
c) Finally show that,
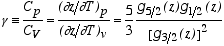
From the above, show that as T approaches the condensation temperature Tc from above, both  and Cp diverge as 1/(T-Tc). and Cp diverge as 1/(T-Tc).
Hint: to show the first identity above, consider the specific heats per particle C/N. [10 pts]
- Problem 2 [35 points total]
Consider a gas with hard core inter-particle interactions, i.e.
| u(r) | = | infinity
0 | for r<ro
for r>ro |
(a) Compute the 2nd and 3rd virial coefficients, B2 and B3 for d=1 dimension (hard rods). [7 points]
(b) Do the same for d=2 dimensions (hard disks). [7 points]
(c) Compute the isothermal compressibility,  T, in terms of the virial expansion to 2nd order, i.e. through B2 and B3. [7 points] T, in terms of the virial expansion to 2nd order, i.e. through B2 and B3. [7 points]
(d) Compute the specific heat at constant pressure, Cp, in terms of the virial expansion to 2nd order, i.e. through B2 and B3. (Hint: to compute Cp you might wish to use the formula that relates it to CV,  T, and the coefficient of thermal expansion T, and the coefficient of thermal expansion  .) [7 points] .) [7 points]
(e) Using your results in parts (a) and (b), and using Pathria Eqs. (9.3.15) and (9.3.20) to get B2 and B3 for hard spheres in d=3 dimensions, make a table showing how  T and Cp-CV vary with dimension d for hard core interactions. Comment on any trends you see. [7 points] T and Cp-CV vary with dimension d for hard core interactions. Comment on any trends you see. [7 points]
|

