|
|

Home
Contact
Info
Course
Info
Calendar
Homework
Lecture
Notes
|
|
|
|
Physics 418: Statistical Mechanics I
Prof. S. Teitel stte@pas.rochester.edu ----- Spring 2006
Problem Set 3
Due Tuesday, March 21, in lecture
- Problem 1 [20 points total]
Consider a classical gas of N indistinguishable non-interacting
particles with ultrarelativistic energies, i.e. their kinetic energy -
momentum relation is given by  = pc, with c the speed of light and p the
magnitude of the particle's momentum. The gas is confined to a box of volume V. = pc, with c the speed of light and p the
magnitude of the particle's momentum. The gas is confined to a box of volume V.
(a) Compute the canonical partition function for this system. [5 points]
(b) Show that this system obeys the usual ideal gas law, pV =
NkBT. [5 points]
(c) Show that the total average energy is, E = 3NkBT
(and hence using (b) gives, E/V = 3p). [5 points]
(d) Show that the ratio of specific heats is, Cp/CV =
4/3. [5 points]
- Problem 2 [20 points total]
In lecture we discussed the canonical ensemble, in which the temperature T, volume V, and number of particle N of a system are fixed, and energy E is allowed to fluctuate. Suppose now that you wish to describe the system by a new ensemble in which the pressure p is fixed, and the volume V is allowed to fluctuate.
a) Define the appropriate partition function Z(T, p, N) of the system in this new constant pressure ensemble. [5 points]
b) If you defined Z properly in part (a), then the Gibbs free energy should be given by
G(T, p, N) = -kBT ln Z(T, p, N)
To demonstrate this, show that using G defined from Z as above, the average volume of the system is correctly given by,
<V> = (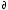 G/ G/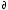 p)T,N [5 points] p)T,N [5 points]
c) Derive a relation, in this constant pressure ensemble, between the isothermal compressibility  T and fluctuations in the volume V of the system. Show from this relation that the relative fluctuation in V vanishes in the thermodynamic limit. [5 points] T and fluctuations in the volume V of the system. Show from this relation that the relative fluctuation in V vanishes in the thermodynamic limit. [5 points]
d) Consider an ideal gas of non-relativistic, non-interacting, point particles of mass m. Explicitly compute the partition function Z(T,p,N) of this gas. Use Z to compute G(T,p,N), and then from G compute the specific heat at constant pressure, Cp. Show that you get the correct answer for the ideal gas. [5 points]
- Problem 3 [5 points total]
The grand canonical ensemble may be described as one in which the
total energy, E, and total number of particles, N, fluctuate, but in which the
total average energy, <E>, and the total average number of particles, <N>,
are fixed. Starting with Shannon's definition of the entropy for a
probability distribution,
S = - kB  i pi ln pi i pi ln pi
determine the grand canonical probabilities pi,
by maximizing the above S subject to the constraints of fixed <E>
and <N>. [5 points]
- Problem 4 [15 points total]
Consider, as a model of the atmosphere of the Earth, an ideal gas in a gravitational potential energy U(r)=mgz. For simplicity, assume the molecules in the gas are all the same and can be taken as indistinguishable point particles with a mass m. The height above the surface is z, and g is the constant of gravitational acceleration. Because the potential energy varies with height z, so will the density n(z) and pressure p(z). The goal of this problem is to find n(z) and p(z) in two different models of the atmosphere.
a) Assume a model of an isothermal atmosphere, where the temperature T is independent of the height z. Find the density n(z) and the pressure p(z) as a function of height. Write your answers in terms of T and the pressure at the surface, p(0). [5 points]
Hint: It is easy to find n(z) - just think about the Boltzmann factor. To find p(z), consider the atmosphere to be divided into slabs of small thickness  z and show that the ideal gas law applies locally within each slab. z and show that the ideal gas law applies locally within each slab.
b)
Assume now a model of an isentropic atmosphere, i.e. one in which the entropy per particle S/N is independent of height. Find how the density n(z), the pressure p(z) and the temperature T(z) must vary with height in such a model. Write your answers in terms of the temperature and pressure at the surface, T(0) and p(0). [10 points]
Hint: Consider the atmosphere to be divided up into slabs, as in the hint to part (a). Compute the partition function for the slab at height z (you can use whichever ensemble you like) and find n(z), p(z) and S(z) in terms of the parameters of the partition function. Then apply the isentropic condition that S(z)/N(z) is independent of z (where N(z)=Vn(z), with V the volume of the slab) to derive relations between n(z), p(z) and T(z). Finally, use the condition of hydrostatic equilibrium,
dp/dz = -mng,
to find T(z) and hence n(z) and p(z). (The equation of hydrostatic equilibrium comes from requiring that the net force on the slab at height z should vanish.)
|

