|
|

Home
Contact
Info
Course
Info
Calendar
Homework
Lecture
Notes
|
|
|
|
Physics 418: Statistical Mechanics I
Prof. S. Teitel stte@pas.rochester.edu ----- Spring 2006
Problem Set 5
Due Friday, April 14, in lecture
- Problem 1 [15 points total]
In lecture we saw that the quantum N particle canonical
partition function could be written as a series involving
0-particle, 2-particle, 3-particle, ...,and N-particle exchanges.
The first two terms in this series were,
| QN(T,V) = |
(VN/
N!  3N) 3N) |
[ 1 ± V -2 |

i<j |
 |
d3ri |
 |
d3rj |
f(ri-rj)
f(rj-ri) |
] |
where
f(r)=e- r2/ r2/ 2 and 2 and  is the thermal wavelength. The (+) sign is for bosons, and the (-) sign is for fermions.
The first term above gives the classical partition function, while
the second term can be viewed as the leading quantum correction
(in the limit that quantum corrections are small).
For the calculations below,
you may assume that this quantum correction term is small. is the thermal wavelength. The (+) sign is for bosons, and the (-) sign is for fermions.
The first term above gives the classical partition function, while
the second term can be viewed as the leading quantum correction
(in the limit that quantum corrections are small).
For the calculations below,
you may assume that this quantum correction term is small.
a) Explicitly evaluate the integrals to compute the above partition function. [5 pts]
b) Find the corresponding Helmholtz free energy. [5 pts]
c) Using your result in part (b), find the corresponding equation of state. How does the leading quantum
correction change the usual ideal gas law, pV = NkBT? [5 pts]
- Problem 2 [10 points total]
Consider photons of a given energy  = = 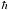  . .
(a) If <n> is the average number of such photons in equilibrium
at temperature T, show that the fluctuation in the number of photons is
<n2> - <n>2 = - (1/ ) (d<n>/d ) (d<n>/d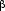 )
where )
where 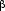 = 1/kBT = 1/kBT
[5 pts]
(b) Using the forumula for the equilibrium value of <n>,
apply the above result to determine the relative fluctuation in the number
of photons
[<n2> - <n>2]/<n>2
Is this large or small? [5 pts]
- Problem 3 [20 points]
In the grand canonical ensemble, the probability to have a given state "a"
with total energy Ea and total number of particles Na
is,
Pa =
[e-(Ea-µNa)/kBT]/L
where
L = 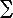 a [e-(Ea-µNa)/kBT]
is the grand canonical partition function. a [e-(Ea-µNa)/kBT]
is the grand canonical partition function.
(a) For a quantum ideal gas, with single particle states i of energy
 i, many particle states are specified by the occupation
numbers {ni} and have energy E = i, many particle states are specified by the occupation
numbers {ni} and have energy E = 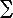 i
[ i
[ ini]. Show that the probability for the state with
occupations {ni} is given by ini]. Show that the probability for the state with
occupations {ni} is given by
P({ni}) = 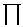 i [pi(ni)] i [pi(ni)]
where pi(ni) is the probability that single particle
state i has occupation ni
pi(ni) =
[e-( i-µ)ni/kBT]/wi i-µ)ni/kBT]/wi
where
wi = 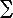 ni [e-( ni [e-( i-µ)ni/kBT] i-µ)ni/kBT]
can be thought of as the partition function
for the single particle state i.
The above factorization says that the number of particles ni
in state i, is independent of the number of particles
nj in state j. [5 points]
(b) Using the above result, show that the Shannon definition of entropy can
be written as
S = -kB 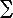 {ni} [P({ni}) ln
P({ni})] = -kB {ni} [P({ni}) ln
P({ni})] = -kB 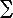 i i
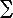 ni [pi(ni) ln
pi(ni)] ni [pi(ni) ln
pi(ni)]
[5 points]
(c) Using the above result, show that the following expressions apply for
the entropies of an ideal gas of bosons and fermions, respectively
| bosons: |
S = kB 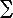 i [(1+<ni>)
ln (1+<ni>) - <ni> ln
<ni>] i [(1+<ni>)
ln (1+<ni>) - <ni> ln
<ni>] |
fermions: |
S = kB 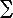 i [-(1-<ni>)
ln (1-<ni>) - <ni> ln
<ni>] i [-(1-<ni>)
ln (1-<ni>) - <ni> ln
<ni>] |
where <ni> = 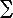 ni
[ni pi(ni)] is the average occupation
number of state i.
[10 points] ni
[ni pi(ni)] is the average occupation
number of state i.
[10 points]
|

