Problem Set 6

Problem Set 6

Due Wednesday, April 16, in lecture

Problem 1

Consider a band with an anisotropic dispersion relation,

ε(k) = (hbar)²
2 ( k_x²
m_x + k_y²
m_y + k_z²
m_z )
a) Using the fact that an ellipsoid given by the equation, (x/a)² + (y/b)² + (z/c)² = 1, encloses a volume (4π/3)abc, calculate the density of states g(ε). Hint: One can write for the density of states, g(ε)=dG(ε)/dε, where G(ε) is the number of single electron states per unit volume with energy less than ε.
b) We learned that, at sufficiently low temperatures, the contribution to the specific heat at constant volume due to the conduction electrons is given by c_v = γ T, where γ is a constant independent of temperature. For the anisotropic band structure considered here, explain why γ is proportional to the effective mass m^* = (m_xm_ym_z)^1/3.
Problem 2
Consider a one dimensional lattice structure consisting of two different atoms A and B that alternate at equally spaced intervals of width a, as sketched below.

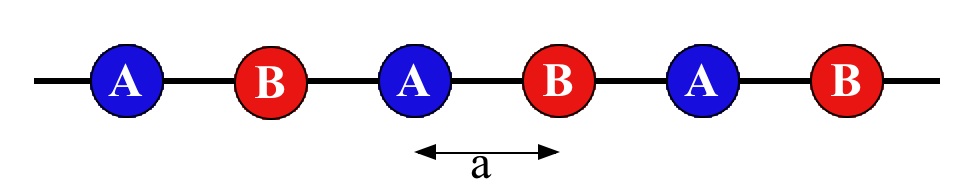
Assume that each atom contributes one valence electron. For atoms centered at the origin, the atomic orbital of an A atom valence electron is φ_A(r) and the atomic orbital of a B atom valence electron is φ_B(r). The atomic energy levels of these orbitals are E_A and E_B respectively. You may assume that φ_A and φ_B are real and spherically symmetric.
Using the tight binding method, compute the band structure energies and eigenstates for this lattice. Assume that only nearest neighbor overlap integrals are significant.
Plot the band energies vs k in the first Brillouin Zone.
Problem 3
Using the tight binding band structure for the π and π* bands of graphene as computed in lecture, show:
a) For k near k=0, the surfaces of constant energy are circles centered about the orign.
b) For k near k_K at a vertex of the surface of the first Brillouin Zone, show that the band energies are ε_±(k) ~ |k−k_K|.
c) For k near k_K at a vertex of the surface of the first Brillouin Zone, show that the surfaces of constant energy are circles centered about k_K.
d) Find an energy ε for which the surface of constant energy ε is strongly nested. Draw this surface in the first Brillouin Zone.
e) Compute the density of states g(ε) for ε near ε_F, and show that it vanishes linearly as ε approaches ε_F. Recall that for graphene, the Fermi surface consists of the 6 vertex points on the surface of the first Brillouin Zone.