Introduction

A sample cluster performed with the cone algorithm is shown below. The green spheres are the particles identified as on the surface, and yellow ones are inside.

Downloading source code

1. the source code will only be used for academic or personal purpose, not commercial purpose.
2. the author is not responsible for any consequences caused by the usage of this code.
3. if the usage of this code leads to publishable research results, you will cite the original publication describing this algorithm: Yanting Wang, S. Teitel, and Christoph Dellago, Melting of Icosahedral Gold Nanoclusters from Molecular Dynamics Simulations J. Chem. Phys. 122 214722-214738, 2005.

Basic idea

In order to tell computer how to pick up surface particles according to their positions, one quantified expression equivalent to the above criteria is:

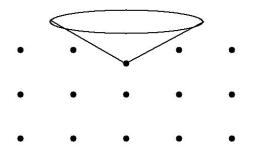
For a given particle, its associated cone region is defined as the region inside a cone of a certain side length and angle, whose vertex resides on the particle. A hollow cone is a cone region with no other particles inside it. A particle is identified as on the surface if at least one associated hollow cone exists.

There are two adjustable parameters for the cone: angle and side length. The accuracy (or satisfactory) of the results depends on these two parameters. This algorithm is immediately applicable to the situations when there are multiple molecules in one configuration and/or there are holes inside molecules.

Implementation

• The cell index method is employed to accelerate the identification of neghiboring particles. The side length of cell is a little larger than the side length of the cone (also noted as cutoff). Neighboring particles are determined as those within the cutoff distance.
• In order to determine if there exists a hollow cone for a given particle, we should loop over all the combinations of 3 of its neighboring particles to see if other neighboring particles are in it. The scalar products of the vectors connecting these particles are used to determine if a cone region spanned by 3 particles are big enough for the given two parameters and if other particles are inside the cone region. Be sure that the opposite cone defined by the same vectors are also checked at the same time.
• In order to identify a surface particle, finding the existence of one hollow cone is enough and the loop can then be terminated. In contrast, to identify an internal particle requires a complete search of all of the three-neighbor combinations to assert no hollow cones exist.
  This simple method is complete but time consuming. Several methods mentioned below enhance the computational speed drastically.

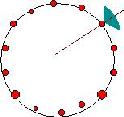
• Actually most internal particles far from surface can be identified by a much easier way according to the definition that they are all surrounded by other partciles: for a certain cell(red), look at designated neighbor cells(blue); if all of them contain particles, all of the particles in this certain cell are all internal. The right image shows the 2D case. More cells have to be checked in 3D.

• Some surface particles can also be pre-identified by the global geometry of the cluster. For example, if the cluster has a rounded shape, it has a good chance that a hollow cone can be found simply by choosing the vector from the center to the particle as the principle axis of a cone region.

• The remained undetermined particles have to go through the above complete loop-over algorithm. However, we can still do something with the neighboring particles during the loop-over:
  1. Neighboring particles already identified as internal do not have to join the loop-over procedure.
  2. Because there is a better chance that a hollow cone can be found among surface particles, first loop over the combinations of 3 surface particles, then 2 surface and 1 undetermined, then 1 surface and 2 undetermined, finally 3 undetermined.

Programming

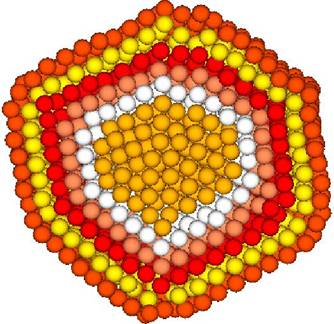
Multi-layer identification

Back to Yanting Wang's Homepage

You are the visitor since July 18, 2008.