 Lunar
Lunar
Tides
The
tides
at a given place in the Earth's oceans occur
about an hour later each day. Since the Moon passes overhead about an hour
later each day, it was long suspected that the Moon was associated with tides.
Newton's Law of Gravitation
provided a quantitative understanding of
that association.
Differential Forces
Consider a water molecule in the ocean. It is
attracted gravitationally
by the
Earth, but it also experiences a much smaller gravitational attraction from the
Moon (much smaller because the Moon is much further away and much less massive
than the Earth). But this gravitational attraction of the Moon is not limited
to the water molecules; in fact, the Moon exerts a gravitational force on every
object on and in the Earth. Tides occur
because the Earth is a body of finite extent and these forces are not uniform: some
parts of the Earth are closer to the Moon than other parts, and since the
gravitational force is weaker with increasing distance those parts
experience a larger gravitational tug from the Moon
than parts that are further away.
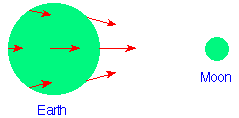 In this situation, which is illustrated schematically in the adjacent figure,
we say that differential forces act on the body (the Earth in this
example). The effect of differential forces on a body
is to distort the body. The body of
the Earth is rather rigid, so such distortion effects are small (but finite).
However, the fluid in the Earth's oceans is much more easily deformed and this
leads to significant tidal effects.
In this situation, which is illustrated schematically in the adjacent figure,
we say that differential forces act on the body (the Earth in this
example). The effect of differential forces on a body
is to distort the body. The body of
the Earth is rather rigid, so such distortion effects are small (but finite).
However, the fluid in the Earth's oceans is much more easily deformed and this
leads to significant tidal effects.
A Simple Tidal Model
We may illustrate the basic idea with a simple model of a planet completely
covered by an ocean of uniform depth, with negligible friction between the
ocean and the underlying planet, as illustrated in the adjacent figure.
The gravitational
attraction of the Moon produces two tidal bulges on opposite sides of the
Earth.
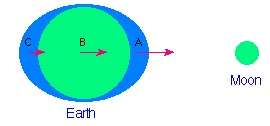 Without getting too much into the technical details, there are two
bulges because of the differential gravitational forces. The liquid at point A
is closer to the Moon and experiences a larger gravitational force than the
Earth at point B or the ocean at point C. Because it experiences a larger
attraction, it is pulled away from the Earth, toward the Moon, thus producing
the bulge on the right side. Loosely, we may think of the bulge on the left
side as arising because the Earth is pulled away from the water on that side
because the gravitational force exerted by the Moon at point B is larger than
that exerted at point C.
Then, as our idealized Earth rotates under these bulges, a given point on
the surface will experience two high and two low tides for each rotation of the
planet.
Without getting too much into the technical details, there are two
bulges because of the differential gravitational forces. The liquid at point A
is closer to the Moon and experiences a larger gravitational force than the
Earth at point B or the ocean at point C. Because it experiences a larger
attraction, it is pulled away from the Earth, toward the Moon, thus producing
the bulge on the right side. Loosely, we may think of the bulge on the left
side as arising because the Earth is pulled away from the water on that side
because the gravitational force exerted by the Moon at point B is larger than
that exerted at point C.
Then, as our idealized Earth rotates under these bulges, a given point on
the surface will experience two high and two low tides for each rotation of the
planet.
The side of the Earth facing the moon is 6400km closer than
the side away. The differential forces are 3% of the moon's
total gravitational force but this is enough to produce the effect.
As we sit on the beach and watch for the
tides, the surface of the earth is actually
rotating underneath the water that is being pulled.
More Realistic Tidal Models
The realistic situation is considerably more complicated:
-
The Earth and
Moon
are not static, as depicted in the preceding diagram, but instead are in
orbit around the common center of mass for the system.
- The Earth is not
covered with oceans, the oceans have varying depths, and there is substantial
friction between the oceans and the Earth.
These make a more realistic
description much more complicated, but the essential ideas remains as
illustrated in the preceding diagram.
Spring Tides and Neap Tides
Another complication of a realistic model is that not only the Moon, but other
objects in the Solar System, influence the Earth's tides. For most their tidal
forces are negligible on Earth, but the differential gravitational force of the
Sun does influence our tides to some degree (the effect of the Sun on Earth
tides is less than half that of the Moon. The Sun is 27 million times
more massive than the moon, but is 400 times farther away.)
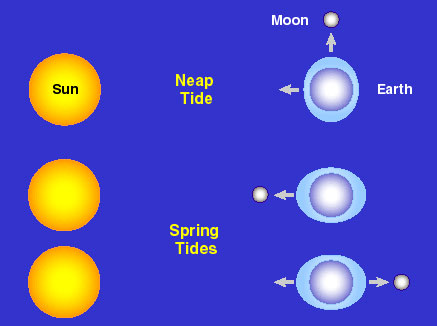 |
|
Competition between the Sun and Moon in producing tides.
|
For example, particularly large
tides are experienced in the Earth's oceans when the Sun and the Moon are lined
up with the Earth at new and full phases of the Moon. These are called
spring tides (the name is not associated with the season of Spring). The
amount of enhancement in
Earth's tides is about the same whether the Sun and Moon are lined
up on opposite sides of the Earth (full Lunar phase) or on the same side (new
Lunar phase).
Conversely, when the Moon is at first quarter or last quarter phase (meaning
that it is located at right angles to the Earth-Sun line), the Sun and Moon
interfere with each other in producing tidal bulges and tides are generally
weaker; these are called neap tides. The figure shown above
illustrates spring and neap tides.
Tidal Coupling and Gravitational Locking
We have introduced tides in terms of the effect of the Moon on the Earth's
oceans, but the effect is much more general, and has a number of important
consequences.
For example, as a consequence of tidal interactions with the Moon,
the Earth is slowly decreasing its rotational period and
eventually the Earth and Moon will have exactly the same rotational period, and
these will also exactly equal the orbital period.
Thus, billions of years from now the Earth
will always keep the same face turned toward the Moon, just as the Moon already
always
keeps the same face turned toward the Earth.
The slow down of Earth's rotation leads to 0.002 extra
seconds per day, about 1 second per year.
Tides also affect orbital motion. The tidal bulges
also pull the moon a little bit ahead in its orbit.
Then the moon is accelerated and it moves out to a larger radius.
The effect moves the moon outward 3.8cm per year.
This can be measured by bouncing laser beams off of the moon
and measuring the time it takes for the signal to return.
Reflectors were left by Apollo astronauts.
 In this situation, which is illustrated schematically in the adjacent figure,
we say that differential forces act on the body (the Earth in this
example). The effect of differential forces on a body
is to distort the body. The body of
the Earth is rather rigid, so such distortion effects are small (but finite).
However, the fluid in the Earth's oceans is much more easily deformed and this
leads to significant tidal effects.
In this situation, which is illustrated schematically in the adjacent figure,
we say that differential forces act on the body (the Earth in this
example). The effect of differential forces on a body
is to distort the body. The body of
the Earth is rather rigid, so such distortion effects are small (but finite).
However, the fluid in the Earth's oceans is much more easily deformed and this
leads to significant tidal effects.
 Lunar
Lunar Without getting too much into the technical details, there are two
bulges because of the differential gravitational forces. The liquid at point A
is closer to the Moon and experiences a larger gravitational force than the
Earth at point B or the ocean at point C. Because it experiences a larger
attraction, it is pulled away from the Earth, toward the Moon, thus producing
the bulge on the right side. Loosely, we may think of the bulge on the left
side as arising because the Earth is pulled away from the water on that side
because the gravitational force exerted by the Moon at point B is larger than
that exerted at point C.
Then, as our idealized Earth rotates under these bulges, a given point on
the surface will experience two high and two low tides for each rotation of the
planet.
Without getting too much into the technical details, there are two
bulges because of the differential gravitational forces. The liquid at point A
is closer to the Moon and experiences a larger gravitational force than the
Earth at point B or the ocean at point C. Because it experiences a larger
attraction, it is pulled away from the Earth, toward the Moon, thus producing
the bulge on the right side. Loosely, we may think of the bulge on the left
side as arising because the Earth is pulled away from the water on that side
because the gravitational force exerted by the Moon at point B is larger than
that exerted at point C.
Then, as our idealized Earth rotates under these bulges, a given point on
the surface will experience two high and two low tides for each rotation of the
planet.
