| > | with(VectorCalculus): with(plots): |
Assume toroidal field can be set up by a radial gradient of a vector potential with only a Z-component
| > | SetCoordinates(cylindrical[s,phi,z]): simplify(Curl(VectorField(<0,0,A(s,z)>))); |
![]()
Invert the curl to get a potential that will give the desired toroidal field.
| > | assume(r_m<1, r_m>0, R>z, z>0,R>0,R>s); |
| > | s:='s'; |
![]()
| > | B_desired:=s->piecewise(s < r_m*sqrt(R^2-z^2), Bo*s/(r_m), Bo*sqrt(R^2-z^2)*(sqrt(R^2-z^2)-s)/(sqrt(R^2-z^2)-r_m*sqrt(R^2-z^2))): Az:=s->(-int(B_desired(r), r=0..s)+int(B_desired(r), r=0..sqrt(R^2-z^2))); |
![]()
![]()
| > | display(plot3d(subs(Bo=1,R=1,r_m=.8,Az(s)), s=0..1.1, z=-1..1, grid=[50,50],view=0..0.5, style=patchnogrid),pointplot3d([seq([cos(2*Pi*i/200),sin(2*Pi*i/200),0], i=0..200)], connect=true, color=black)); |
![[Maple Plot]](images/pot5.gif)
| > | Az(s); |
![-PIECEWISE([1/2*Bo*s^2/r_m, s <= r_m*(R^2-z^2)^(1/2)],[-1/2*Bo*(2*(R^2-z^2)^(1/2)*s-s^2-r_m*R^2+r_m*z^2)/(-1+r_m), r_m*(R^2-z^2)^(1/2) < s])+1/2*Bo*R^2-1/2*Bo*z^2](images/pot6.gif)
| > | B_tor:=Curl(VectorField(<0,0,Az(s)>)); |
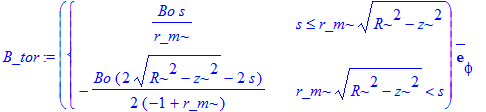
| > | B_tor2:=simplify(B_tor[1]^2+B_tor[2]^2); |
![B_tor2 := PIECEWISE([Bo*s/r_m, s <= r_m*(R^2-z^2)^(1/2)],[Bo*(-(R^2-z^2)^(1/2)+s)/(-1+r_m), r_m*(R^2-z^2)^(1/2) < s])^2](images/pot8.gif)
| > | display(plot3d(subs(Bo=1,R=1,r_m=.8,B_tor[2]), s=0..1, z=-1..1, view=0..1,grid=[50,50],style=patchnogrid),pointplot3d([seq([cos(2*Pi*i/200),sin(2*Pi*i/200),0], i=0..200)], connect=true, color=black)); |
![[Maple Plot]](images/pot9.gif)
| > | SetCoordinates(polar[r,theta]): B3D:=MapToBasis(VectorField( <0,B_tor[2]>, 'polar'[s,theta] ), 'cartesian'[x,y]): |
| > | display(fieldplot(subs({Bo=1,R=1,r_m=.8,z=.6},B3D), x=-1..1, y=-1..1), plot([cos(theta), sin(theta), theta=0..2*Pi])); plot([subs({x=0,Bo=1,R=1,r_m=.8,z=0},B3D[1]^2)], y=0..1); |
![[Maple Plot]](images/pot10.gif)
![[Maple Plot]](images/pot11.gif)
Now for the poloidal field, we assume we can use a toroidal vector potential. Since we want a dipole type field, we set A_phi=A(r)*sin(theta)
| > | SetCoordinates(spherical[r,theta,phi]): simplify(Curl(VectorField(<0,0,Ap(r)*sin(theta)>))); |
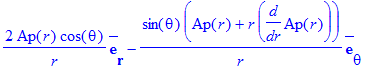
Since we need A_phi to go to zero at r=0 and we need A_phi to go to zero as well as B_pol to go to zero at r=R-r , we try
| > | Ap:=Bo/(2*R^2)*r*(R-r)^2; |
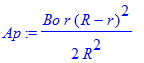
| > | plot(subs(Bo=1,R=1,Ap(r)), r=0..1); |
![[Maple Plot]](images/pot14.gif)
| > | B_pol:=simplify(Curl(VectorField(<0,0,Ap*sin(theta)>))); |
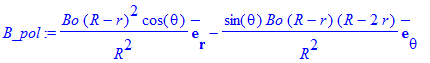
| > | B_pol2:=simplify(B_pol[1]^2+B_pol[2]^2); |
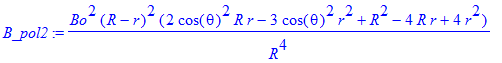
| > | SetCoordinates(polar[r,theta]): B3D:=MapToBasis(VectorField( <B_pol[1],B_pol[2]>, 'polar'[r,theta] ), 'cartesian'[x,y]): display(fieldplot(subs({Bo=1,R=1},B3D), x=-1..1, y=-1..1), plot([cos(theta), sin(theta), theta=0..2*Pi])); plot([subs({x=0,Bo=1,R=1},B3D[1]^2)], y=0..1); |
![[Maple Plot]](images/pot17.gif)
![[Maple Plot]](images/pot18.gif)
| > |