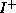 , the future domain of
dependence
(definition
, the future domain of
dependence
(definition
As we have seen before the important notion for the domain of influence is precedes. Now we can ask how what is happening in some region is related with an other region. Here it is not a point to point relation. We need to register all the signal that can influence p. The mathematical object used is the slice .
The physical situation on 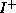 , the future domain of
dependence
(definition
, the future domain of
dependence
(definition ![]() page
page ![]() ) is
completely determined by the information on S.
) is
completely determined by the information on S.
There is some interesting properties of the domain of
dependence. The main one is that it is internally causally
compact i.e. for every p and q in  the closure of
the closure of
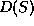 is compact. This reflect the fact
that there is no holes in
is compact. This reflect the fact
that there is no holes in 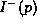 .
Another property is that for p preceding q there exists a
timelike geodesic of maximal length from p to q.
.
Another property is that for p preceding q there exists a
timelike geodesic of maximal length from p to q.
This idea of domain of dependence is link with
determinism
in the spacetime. It is closely related with Cauchy
surface. S is said to be a Cauchy surface
if 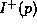 , in
other word the single slice S is enough to determine what
happens in the entire spacetime.
, in
other word the single slice S is enough to determine what
happens in the entire spacetime.
Ask for a Cauchy surface is a very strong condition upon the
spacetime. If a spacetime has a Cauchy surface then it must be
stably causal .
Even more the time-function can be chosen in a
such way that the slice of constant t is a Cauchy surface,
in particular there is a Cauchy surface passing through every
point. In addition all the slice must be diffeomorphic.
The idea of a Cauchy surface is that it is predictive, one can determine the physics in all the spacetime from the initial conditions. But at the same time there are a lot of spacetime without Cauchy surfaces, one can think about them at being less controllable, there are influences that come from other regions.
Then in what sense the existence of a Cauchy surface is a physically reasonable requirement? In other word can we just rule out the non-predictive spacetime? There is no firm answer yet but there is work to show that spacetime without Cauchy surface are unstable and therefore with less interest.
One way to show that a slice is a Cauchy surface is to use the
notion of Cauchy horizon . The future Cauchy
horizon (definition ![]() page
page ![]() ) of an
achronal slice (definition
) of an
achronal slice (definition ![]() page
page ![]() ) is the collection of all points p of
) is the collection of all points p of
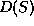 which precedes no point of
which precedes no point of 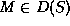 . It is like
the future boundary of
. It is like
the future boundary of 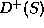 . The future Cauchy
horizon is always an achronal set. There is also a past
Cauchy horizon .
An achronal slice is a Cauchy surface if, and only if, its
future and past Cauchy horizon are both empty.
. The future Cauchy
horizon is always an achronal set. There is also a past
Cauchy horizon .
An achronal slice is a Cauchy surface if, and only if, its
future and past Cauchy horizon are both empty.
One of the properties of the Cauchy horizon is that it is
null, it means that for p on this horizon there exist a
maximally extended past-directed null geodesic from p which
always stays in this horizon.
The idea of domain of dependence and influence are at the center of the causal structure of spacetimes. Understand these is useful to understand the singularity theorems and therefore the topological censorship.