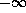 cannot be null geodesically complete if:
cannot be null geodesically complete if:
These theorems prove the existence of singularities in the spacetime in a very general way. The assumptions about the spacetime and the matter are not so restrictive.
Here we will explain in more detail the proof of the theorem 1 of [3, p 263,] . If we take the time to do so it is because the mechanism of that proof is useful for the Topological Censorship .
First we have to give some definitions about the hypotheses of that theorem which say:
A spacetime 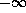 cannot be null geodesically complete if:
cannot be null geodesically complete if:
When we assume that the spacetime has a Cauchy surface we assume that it is globally hyperbolic and causally simple .
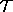
It is equivalent to say that  and
and 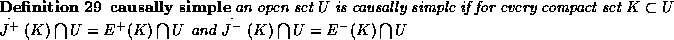 are
closed in U.
are
closed in U.
In order to understand the definition of causally simple one need to define the notation used (Hawking and Ellis [3] notation).
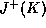
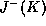
Now that thes definitions are set we can begin to see the
proof in more detail.
The idea of this kind of proof is to study the boundary of the
causal future of the trapped surface
(see section ![]() page
page ![]() )
and find a contradiction
with the hypothesis! It is a rather general method of point
set topology. A similar method is applied to prove the second
lemma of the Topological Censorship .
)
and find a contradiction
with the hypothesis! It is a rather general method of point
set topology. A similar method is applied to prove the second
lemma of the Topological Censorship .
As we assume that the spacetime is causally
simple , the
boundary of  is
is 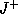 . In other words the boundary of the causal
future of the trapped surface
. In other words the boundary of the causal
future of the trapped surface 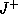 is generated by null geodesics
with end points on the trapped surface and perpendicular to
it.
is generated by null geodesics
with end points on the trapped surface and perpendicular to
it.
From the hypothesis 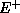 and the
existence of the trapped surface
and the
existence of the trapped surface 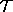 (which mean that
(which mean that
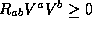 on
on 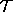 ) we know that
there will be conjugate points because of the Raychaudhuri equation (see section
) we know that
there will be conjugate points because of the Raychaudhuri equation (see section ![]() page
page ![]() ).Because of the
conjugate points geodesics need to stop. But if we look to the boundary
of the causal future there is an end point!
).Because of the
conjugate points geodesics need to stop. But if we look to the boundary
of the causal future there is an end point!
Take the continuous map 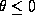 (where Q is the ensemble
(where Q is the ensemble 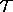 ) which associate to each point p on
) which associate to each point p on 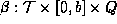 with an affine distance
with an affine distance 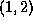 along one of the directed null geodesics from
along one of the directed null geodesics from 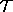 .
As
.
As 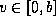 is compact there will be a limit on the value of
is compact there will be a limit on the value of 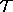 , so this gives an upper limit on
, so this gives an upper limit on 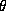 .
.
Form this limit we have, 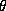 is a compact region.
Then the boundary of the causal future will be compact as a closed
subset of a compact set.
is a compact region.
Then the boundary of the causal future will be compact as a closed
subset of a compact set.
There is not yet a contradiction but as the Cauchy surface is not compact there will be a problem. One cannot cover all of a non-compact space by a compact set! It is like excising a part of the spacetime, so it is not geodesically complete! Therefore there is a contradiction and the assumption is false