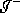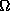 to
to
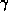 is homotopic to a topologically trivial curve from
is homotopic to a topologically trivial curve from
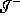 to
to 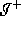 .
.
All 3-manifolds are known to occur as Cauchy surfaces of asymptotically
flat vacuum spacetimes and of spacetimes with positive-energy sources.
We prove here the conjecture that general relativity does not allow an
observer to probe the topology of spacetime: any topological structure
collapses too quickly to allow light to traverse it. More precisely,
in a globally hyperbolic, asymptotically flat spacetime satisfying the
null energy condition, every causal geodesic from 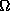 to
to
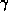 is homotopic to a topologically trivial curve from
is homotopic to a topologically trivial curve from
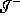 to
to 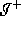 .
.